题目内容
 李爷爷借助如图所示的直角墙角(两边足够长),用32m长的篱笆围成一个矩形花园,想在里面种些花草,篱笆只围AB、BC两边.
李爷爷借助如图所示的直角墙角(两边足够长),用32m长的篱笆围成一个矩形花园,想在里面种些花草,篱笆只围AB、BC两边.(1)若花园的面积为252m2,求AB的长度;
(2)若在P处有一棵树,与墙CD、AD的距离分别是17m和8m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积S的最大值.
考点:二次函数的应用
专题:
分析:(1)根据AB=x米可知BC=(32-x)米,再根据矩形的面积公式即可得出结论;
(2)根据P处有一棵树与墙CD、AD的距离分别是18米和8米求出x的取值范围,再根据(1)中的函数关系式即可得出结论;
(2)根据P处有一棵树与墙CD、AD的距离分别是18米和8米求出x的取值范围,再根据(1)中的函数关系式即可得出结论;
解答:
解:(1)设AB=x米可知BC=(32-x)米,根据题意得:x(32-x)=252.
解这个方程得:x1=18,x2=14,
答:AB的长度18m或14m.
(2)设周围的矩形面积为S,
则S=x(32-x)=-(x-16)2+256.
∵在P处有一棵树与墙CD,AD的距离是17m和8米,
∴8≤x≤15.
∴当x=15时,S最大=-(15-16)2+256=255(平方米).
答:花园面积的最大值是255平方米.
解这个方程得:x1=18,x2=14,
答:AB的长度18m或14m.
(2)设周围的矩形面积为S,
则S=x(32-x)=-(x-16)2+256.
∵在P处有一棵树与墙CD,AD的距离是17m和8米,
∴8≤x≤15.
∴当x=15时,S最大=-(15-16)2+256=255(平方米).
答:花园面积的最大值是255平方米.
点评:本题考查的是二次函数的应用,熟知矩形的面积公式及二次函数的增减性是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,是用两个同样大小的长方体搭成的几何体,这个几何体的左视图是( )
如图,是用两个同样大小的长方体搭成的几何体,这个几何体的左视图是( )A、 |
B、 |
C、 |
D、 |
已知a,b,c是△ABC的边,且a2+b2+c2+50=6a+8b+10c,则c边上的中线为( )
A、
| ||
B、
| ||
C、
| ||
| D、5 |
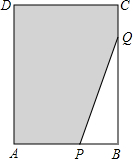 如图,在长方形ABCD中,AB=6,CB=8,点P与点Q分别是AB,CB边上的动点,点P与点Q同时出发,点P以每秒2个单位长度的速度从点A→点B运动,点Q以每秒1个单位长度的速度从点C→点B运动.当其中一个点到达终点时,另一个点也随之停止运动.设运动时间为t秒,阴影部分的面积为Sm2.
如图,在长方形ABCD中,AB=6,CB=8,点P与点Q分别是AB,CB边上的动点,点P与点Q同时出发,点P以每秒2个单位长度的速度从点A→点B运动,点Q以每秒1个单位长度的速度从点C→点B运动.当其中一个点到达终点时,另一个点也随之停止运动.设运动时间为t秒,阴影部分的面积为Sm2.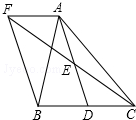 如图,在△ABC中,D是BC边上一点,E是AD的中点,过A作BC的平行线交CE的延长线F,且AF=BD,连结BF.
如图,在△ABC中,D是BC边上一点,E是AD的中点,过A作BC的平行线交CE的延长线F,且AF=BD,连结BF. 如图,由24个边长为1的正方形组成4×6的网格.若△A′B′C′∽△ABC(相似比不是1),且△A′B′C′,△ABC的顶点都是网格内正方形的顶点,则△A′B′C′的面积是
如图,由24个边长为1的正方形组成4×6的网格.若△A′B′C′∽△ABC(相似比不是1),且△A′B′C′,△ABC的顶点都是网格内正方形的顶点,则△A′B′C′的面积是