题目内容
3.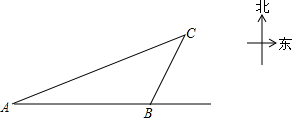 一艘轮船自西向东航行,在A处测得北偏东68.7°方向有一座小岛C,继续向东航行22海里到达B处,测得小岛C此时在轮船的北偏东26.5°方向上,而小岛C方圆10海里的范围内有暗礁,轮船继续向东航行有无触礁的危险呢?请说明理由.(参考数据:sin21.3°≈$\frac{9}{25}$,tan21.3°≈$\frac{2}{5}$,sin63.5°≈$\frac{9}{10}$,tan63.5°≈2)
一艘轮船自西向东航行,在A处测得北偏东68.7°方向有一座小岛C,继续向东航行22海里到达B处,测得小岛C此时在轮船的北偏东26.5°方向上,而小岛C方圆10海里的范围内有暗礁,轮船继续向东航行有无触礁的危险呢?请说明理由.(参考数据:sin21.3°≈$\frac{9}{25}$,tan21.3°≈$\frac{2}{5}$,sin63.5°≈$\frac{9}{10}$,tan63.5°≈2)
分析 首先过点C作CD⊥AB于点D,由题意得:AB=22,∠CAB=21.3°,∠CBD=63.5°,然后在Rt△CBD中,tan∠CBD=$\frac{CD}{BD}$,可得BD=$\frac{1}{2}$CD,又由在Rt△ACD中,tan∠CAB=$\frac{CD}{AD}$,可得$\frac{CD}{22+\frac{1}{2}CD}$=$\frac{2}{5}$,继而求得CD的长,则可知轮船继续向东航行有无触礁的危险.
解答  解:轮船继续向东航行无触礁的危险.
解:轮船继续向东航行无触礁的危险.
理由:过点C作CD⊥AB于点D,
由题意得:AB=22,∠CAB=21.3°,∠CBD=63.5°,
在Rt△CBD中,tan∠CBD=$\frac{CD}{BD}$,
即$\frac{CD}{BD}$≈2,
∴BD=$\frac{1}{2}$CD,
在Rt△ACD中,tan∠CAB=$\frac{CD}{AD}$,
即$\frac{CD}{22+\frac{1}{2}CD}$=$\frac{2}{5}$,
解得:CD=11>10,
∴轮船继续向东航行无触礁的危险.
点评 此题考查了方向角问题.注意准确构造直角三角形并解直角三角形是关键.

练习册系列答案
相关题目
11.若不等式组$\left\{\begin{array}{l}{1+x<a}\\{3-x≤0}\end{array}\right.$有解,则实数a的取值范围是( )
| A. | a<4 | B. | a≤4 | C. | a>4 | D. | a≥4 |
15.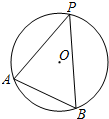 如图,A,B,P是半径为2的⊙O上的三点,∠APB=45°,则弦AB的长为( )
如图,A,B,P是半径为2的⊙O上的三点,∠APB=45°,则弦AB的长为( )
 如图,A,B,P是半径为2的⊙O上的三点,∠APB=45°,则弦AB的长为( )
如图,A,B,P是半径为2的⊙O上的三点,∠APB=45°,则弦AB的长为( )| A. | 2 | B. | 4 | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
12.某射击教练对甲、乙两个射击选手的5次成绩(单位:环)进行了统计,如表
所示:设甲、乙两人射击成绩的平均数分别为$\overline{{x}_{甲}}$、$\overline{{x}_{乙}}$,射击成绩的方差分别为${s_甲}^2$、${s_乙}^2$,则下列判断中正确的是( )
| 甲 | 10 | 9 | 8 | 5 | 8 |
| 乙 | 8 | 8 | 7 | 9 | 8 |
| A. | $\overline{{x}_{甲}}$<$\overline{{x}_{乙}}$,${s_甲}^2$>${s_乙}^2$ | B. | $\overline{{x}_{甲}}$=$\overline{{x}_{乙}}$,${s_甲}^2$<${s_乙}^2$ | ||
| C. | $\overline{{x}_{甲}}$=$\overline{{x}_{乙}}$,${s_甲}^2={s_乙}^2$ | D. | $\overline{{x}_{甲}}$=$\overline{{x}_{乙}}$,${s_甲}^2$>${s_乙}^2$ |
13.为了倡导绿色出行,某市为市民提供了自行车租赁服务,其收费标准如下:
如果小明某次租赁自行车3小时,缴费14元,请判断小明该次租赁自行车所在地区的类别是B类(填“A、B、C”中的一个).
| 地区类别 | 首小时内 | 首小时外 | 备注 |
| A类 | 1.5元/15分钟 | 2.75元/15分钟 | 不足15分钟时 按15分钟收费 |
| B类 | 1.0元/15分钟 | 1.25元/15分钟 | |
| C类 | 免费 | 0.75元/15分钟 |
