题目内容
15.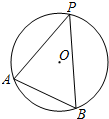 如图,A,B,P是半径为2的⊙O上的三点,∠APB=45°,则弦AB的长为( )
如图,A,B,P是半径为2的⊙O上的三点,∠APB=45°,则弦AB的长为( )| A. | 2 | B. | 4 | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
分析 首先连接OA,OB,由圆周角定理即可求得∠AOB=90°,又由OA=OB=2,利用勾股定理即可求得弦AB的长.
解答  解:连接OA,OB,
解:连接OA,OB,
∵∠APB=45°,
∴∠AOB=2∠APB=90°,
∵OA=OB=2,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=2$\sqrt{2}$.
故选D.
点评 此题考查了圆周角定理以及勾股定理.注意准确作出辅助线是解此题的关键.

练习册系列答案
相关题目
6.下列条件中,可以确定△ABC和△A′B′C′全等的是( )
| A. | BC=BA,B′C′=B′A′,∠B=∠B′ | B. | ∠A=∠B′,AC=A′B′,AB=B′C′ | ||
| C. | ∠A=∠A′,AB=B′C′,AC=A′C′ | D. | BC=B′C′,AC=A′B′,∠B=∠C′ |
10. 如图,数轴上有A,B,C,D四个点,其中表示-3的相反数的点是( )
如图,数轴上有A,B,C,D四个点,其中表示-3的相反数的点是( )
 如图,数轴上有A,B,C,D四个点,其中表示-3的相反数的点是( )
如图,数轴上有A,B,C,D四个点,其中表示-3的相反数的点是( )| A. | 点A | B. | 点B | C. | 点C | D. | 点D |
7.若a<0,则不等式组$\left\{\begin{array}{l}{3x>a}\\{2x>a}\end{array}\right.$的解集是( )
| A. | x>-$\frac{a}{2}$ | B. | x>-$\frac{a}{3}$ | C. | x>$\frac{a}{3}$ | D. | x>$\frac{a}{2}$ |
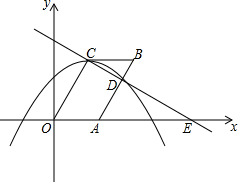 如图,在平面直角坐标系xOy中,抛物线y=-$\frac{2\sqrt{3}}{9}$(x-$\frac{3}{2}$)2+$\frac{3\sqrt{3}}{2}$的顶点为C,连结OC,将线段OC沿x轴的正方向平移到AB交已知抛物线于点D,直线CD交x轴于点E,连结BC.
如图,在平面直角坐标系xOy中,抛物线y=-$\frac{2\sqrt{3}}{9}$(x-$\frac{3}{2}$)2+$\frac{3\sqrt{3}}{2}$的顶点为C,连结OC,将线段OC沿x轴的正方向平移到AB交已知抛物线于点D,直线CD交x轴于点E,连结BC.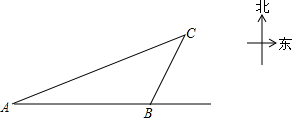 一艘轮船自西向东航行,在A处测得北偏东68.7°方向有一座小岛C,继续向东航行22海里到达B处,测得小岛C此时在轮船的北偏东26.5°方向上,而小岛C方圆10海里的范围内有暗礁,轮船继续向东航行有无触礁的危险呢?请说明理由.(参考数据:sin21.3°≈$\frac{9}{25}$,tan21.3°≈$\frac{2}{5}$,sin63.5°≈$\frac{9}{10}$,tan63.5°≈2)
一艘轮船自西向东航行,在A处测得北偏东68.7°方向有一座小岛C,继续向东航行22海里到达B处,测得小岛C此时在轮船的北偏东26.5°方向上,而小岛C方圆10海里的范围内有暗礁,轮船继续向东航行有无触礁的危险呢?请说明理由.(参考数据:sin21.3°≈$\frac{9}{25}$,tan21.3°≈$\frac{2}{5}$,sin63.5°≈$\frac{9}{10}$,tan63.5°≈2)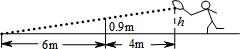 在阳光体育课上,小腾在打网球,如图所示,网高0.9m,球刚好打过网,而且落在离网6m的位置上,则球拍击球的高度h=1.5m.
在阳光体育课上,小腾在打网球,如图所示,网高0.9m,球刚好打过网,而且落在离网6m的位置上,则球拍击球的高度h=1.5m. 如图,已知函数y=2x和函数y=$\frac{k}{x}$的图象交于A、B两点,过点A作AE⊥x轴于点E,若△AOE的面积为4.
如图,已知函数y=2x和函数y=$\frac{k}{x}$的图象交于A、B两点,过点A作AE⊥x轴于点E,若△AOE的面积为4. 如图所示,已知函数y=x+b和y=ax-1的图象交点为M,则不等式x+b<ax-1的解集为x<-1.
如图所示,已知函数y=x+b和y=ax-1的图象交点为M,则不等式x+b<ax-1的解集为x<-1.