Question

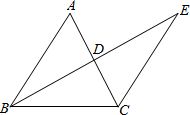如图，BE⊥AC，垂足为D，且AD=CD，BD=ED，若∠ABC=54°，则∠E=

 

°．

Answer 1

考点：全等三角形的判定与性质

专题：计算题

分析：由BE垂直于AC，且AD=CD，利用线段垂直平分线定理得到AB=CB，即三角形ABC为等腰三角形，利用三线合一得到BE为角平分线，求出∠ABE度数，利用SAS得到三角形ABD与三角形CED全等，利用全等三角形对应角相等即可求出∠E的度数．

解答：解：∵BE⊥AC，AD=CD，
∴AB=CB，即△ABC为等腰三角形，
∴BD平分∠ABC，即∠ABE=∠CBE=

1

2

∠ABC=27°，
在△ABD和△CED中，

AD=CD ∠ADB=∠CDE BD=ED

，
∴△ABD≌△CED（SAS），
∴∠E=∠ABE=27°，
故答案为：27

点评：此题考查了全等三角形的判定与性质，熟练掌握全等三角形的判定与性质是解本题的关键．