题目内容
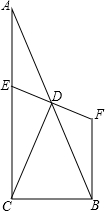 如图,在△ABC中,∠ACB=90°,点D是AB的中点,点E在AC上,点E、D、F一条直线上,且ED=FD,
如图,在△ABC中,∠ACB=90°,点D是AB的中点,点E在AC上,点E、D、F一条直线上,且ED=FD,(1)求证:AE=FB;
(2)若EF⊥CD,且AC=4,CB=2,求CE的长.
考点:全等三角形的判定与性质
专题:计算题
分析:(1)由D为AB的中点,得到AD=BD,再由对顶角相等,利用SAS即可得证;
(2)连接CF,由题意得到CD垂直平分EF,得到CE=CF,设CE=CF=x,则有BAE=AC-EC=4-x,在直角三角形CFB中,利用勾股定理列出关于x的方程,求出方程的解得到x的值,即为CE的长.
(2)连接CF,由题意得到CD垂直平分EF,得到CE=CF,设CE=CF=x,则有BAE=AC-EC=4-x,在直角三角形CFB中,利用勾股定理列出关于x的方程,求出方程的解得到x的值,即为CE的长.
解答: (1)证明:∵D为AB的中点,
(1)证明:∵D为AB的中点,
∴AD=BD,
在△AED和△BFD中,
,
∴△AED≌△BFD(SAS),
∴AE=FB;
(2)解:连接CF,
∵D为EF中点,CD⊥EF,
∴CE=CF,
在Rt△CBF中,设CF=CE=x,FB=AE=AC-EC=4-x,
利用勾股定理得:CF2=CB2+FB2,即x2=4+(4-x)2,
解得:x=2.5,
则CE=2.5.
 (1)证明:∵D为AB的中点,
(1)证明:∵D为AB的中点,∴AD=BD,
在△AED和△BFD中,
|
∴△AED≌△BFD(SAS),
∴AE=FB;
(2)解:连接CF,
∵D为EF中点,CD⊥EF,
∴CE=CF,
在Rt△CBF中,设CF=CE=x,FB=AE=AC-EC=4-x,
利用勾股定理得:CF2=CB2+FB2,即x2=4+(4-x)2,
解得:x=2.5,
则CE=2.5.
点评:此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
正方形具有而菱形不一定具有的性质是( )
| A、内角和为360° |
| B、对角线相等 |
| C、对角线平分内角 |
| D、对角线互相垂直平分 |
下列现象属于平移变换的是( )
| A、足球在草地上滚动 |
| B、钟摆的摆动 |
| C、传送带上,瓶装饮料的移动 |
| D、足球飞入球网中 |
 如图,AB是圆O的直径,弦CD⊥AB于点N,点M在圆O上,C为弧BM的中点.
如图,AB是圆O的直径,弦CD⊥AB于点N,点M在圆O上,C为弧BM的中点. 如图,将一个边长为1的正方形纸片分割成8部分,部分1是边长为1的正方形纸片的一半,部分2是部分1面积的一半,部分3是部分2面积的一半,依此类推.
如图,将一个边长为1的正方形纸片分割成8部分,部分1是边长为1的正方形纸片的一半,部分2是部分1面积的一半,部分3是部分2面积的一半,依此类推. 如图已知,AB∥DC,AB=DC,AE=CF.求证:△ABF≌△CDE.
如图已知,AB∥DC,AB=DC,AE=CF.求证:△ABF≌△CDE.