题目内容
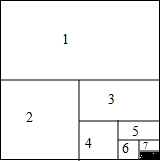 如图,将一个边长为1的正方形纸片分割成8部分,部分1是边长为1的正方形纸片的一半,部分2是部分1面积的一半,部分3是部分2面积的一半,依此类推.
如图,将一个边长为1的正方形纸片分割成8部分,部分1是边长为1的正方形纸片的一半,部分2是部分1面积的一半,部分3是部分2面积的一半,依此类推.(1)阴影部分的面积是
(2)受此启发,直接写出
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 27 |
(3)直接写出
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 2n |
考点:规律型:图形的变化类
专题:
分析:(1)阴影部分的面积等于左下角正方形的面积的一半;
(2)用整个正方形的面积减去阴影部分的面积即可确定答案;
(3)根据前两题将规律整理下来即可.
(2)用整个正方形的面积减去阴影部分的面积即可确定答案;
(3)根据前两题将规律整理下来即可.
解答:解:∵观察图形发现部分1的面积为:
,部分②的面积为:
=
,…,阴影部分的面积
=
,
∴(1)阴影部分的面积是
=
;
(2)
+
+
+…+
=1-
=
;
(3)
+
+
+…+
=1-
,
故答案为:
,
,1-
.
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 4 |
| 1 |
| 27 |
| 1 |
| 128 |
∴(1)阴影部分的面积是
| 1 |
| 27 |
| 1 |
| 128 |
(2)
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 27 |
| 1 |
| 27 |
| 127 |
| 128 |
(3)
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 2n |
| 1 |
| 2n |
故答案为:
| 1 |
| 128 |
| 127 |
| 128 |
| 1 |
| 2n |
点评:本题考查了图形的变化类问题,解题的关键是仔细观察图形并发现图形变化的规律.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
| 1 |
| 2 |
A、
| ||
B、-
| ||
| C、2 | ||
| D、-2 |
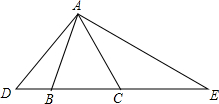 如图,已知△ABC是等边三角形,点D、B、C、E在同一条直线上,且∠DAE=120°.
如图,已知△ABC是等边三角形,点D、B、C、E在同一条直线上,且∠DAE=120°.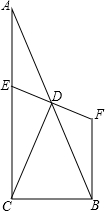 如图,在△ABC中,∠ACB=90°,点D是AB的中点,点E在AC上,点E、D、F一条直线上,且ED=FD,
如图,在△ABC中,∠ACB=90°,点D是AB的中点,点E在AC上,点E、D、F一条直线上,且ED=FD, 在等腰△ABC中,AB=AC.求证:BC边上的高线,中线,∠A的角平分线互相重合.(提示:作BC边上的高AD)
在等腰△ABC中,AB=AC.求证:BC边上的高线,中线,∠A的角平分线互相重合.(提示:作BC边上的高AD)