题目内容
 如图已知,AB∥DC,AB=DC,AE=CF.求证:△ABF≌△CDE.
如图已知,AB∥DC,AB=DC,AE=CF.求证:△ABF≌△CDE.考点:全等三角形的判定
专题:证明题
分析:根据AB∥DC,可得∠C=∠A,然后由AE=CF,得AE+EF=CF+EF,最后利用SAS判定△ABF≌△CDE.
解答:解:∵AB∥DC,
∴∠C=∠A,
∵AE=CF,
∴AE+EF=CF+EF,
在△ABF和△CDE中,
,
∴△ABF≌△CDE(SAS).
∴∠C=∠A,
∵AE=CF,
∴AE+EF=CF+EF,
在△ABF和△CDE中,
|
∴△ABF≌△CDE(SAS).
点评:本题考查了全等三角形的判定,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
| 1 |
| 2 |
A、
| ||
B、-
| ||
| C、2 | ||
| D、-2 |
如果把分式
中的x、y的值都扩大5倍,那么分式的值 ( )
| xy |
| x+y |
| A、扩大5倍 | B、缩小5倍 |
| C、不变 | D、扩大25倍 |
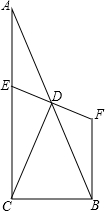 如图,在△ABC中,∠ACB=90°,点D是AB的中点,点E在AC上,点E、D、F一条直线上,且ED=FD,
如图,在△ABC中,∠ACB=90°,点D是AB的中点,点E在AC上,点E、D、F一条直线上,且ED=FD,