题目内容
 如图,AB是圆O的直径,弦CD⊥AB于点N,点M在圆O上,C为弧BM的中点.
如图,AB是圆O的直径,弦CD⊥AB于点N,点M在圆O上,C为弧BM的中点.(1)求证:CB∥MD;
(2)若BC=4,AB=6,求BN的长.
考点:圆周角定理,圆心角、弧、弦的关系,相似三角形的判定与性质
专题:证明题
分析:(1)根据垂径定理,由CD⊥AB得到弧BC=弧BD,加上BC弧=CM弧,则BD弧=CM弧,于是根据圆周角定理可得到∠1=∠M,然后根据平行线的判定即可得到CB∥DM;
(2)连接AC,如图,根据圆周角定理得到∠ACB=90°,再证明Rt△BCN∽Rt△BAC,然后利用相似比可计算出BN的长.
(2)连接AC,如图,根据圆周角定理得到∠ACB=90°,再证明Rt△BCN∽Rt△BAC,然后利用相似比可计算出BN的长.
解答: (1)证明:∵CD⊥AB,
(1)证明:∵CD⊥AB,
∴弧BC=弧BD,
∵C为弧BM的中点,
即BC弧=CM弧,
∴BD弧=CM弧,
∴∠1=∠M,
∴CB∥DM;
(2)解:连接AC,如图,
∵AB为直径,
∴∠ACB=90°,
∵CD⊥AB,
∴∠BNC=90°,BD弧=BC弧,
∴∠BCD=∠BAC,
∴Rt△BCN∽Rt△BAC,
∴
=
,即
=
,
∴BN=
.
 (1)证明:∵CD⊥AB,
(1)证明:∵CD⊥AB,∴弧BC=弧BD,
∵C为弧BM的中点,
即BC弧=CM弧,
∴BD弧=CM弧,
∴∠1=∠M,
∴CB∥DM;
(2)解:连接AC,如图,
∵AB为直径,
∴∠ACB=90°,
∵CD⊥AB,
∴∠BNC=90°,BD弧=BC弧,
∴∠BCD=∠BAC,
∴Rt△BCN∽Rt△BAC,
∴
| BN |
| BC |
| BC |
| AB |
| BN |
| 4 |
| 4 |
| 6 |
∴BN=
| 8 |
| 3 |
点评:本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.也考查了相似三角形的判定与性质.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
 如图,上午8时一条船从A出发(60海里/时)向正东航行,8时30分到B处,经测小岛M在A北偏东45°,在B北偏东30°方向,那么BM的距离为( )
如图,上午8时一条船从A出发(60海里/时)向正东航行,8时30分到B处,经测小岛M在A北偏东45°,在B北偏东30°方向,那么BM的距离为( )A、20(
| ||
B、30
| ||
C、15(
| ||
D、30(
|
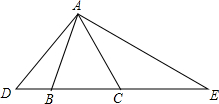 如图,已知△ABC是等边三角形,点D、B、C、E在同一条直线上,且∠DAE=120°.
如图,已知△ABC是等边三角形,点D、B、C、E在同一条直线上,且∠DAE=120°.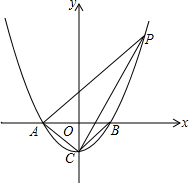 如图,已知抛物线y=x2-1与x轴交于A、B两点,与y轴交于点C
如图,已知抛物线y=x2-1与x轴交于A、B两点,与y轴交于点C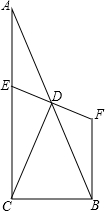 如图,在△ABC中,∠ACB=90°,点D是AB的中点,点E在AC上,点E、D、F一条直线上,且ED=FD,
如图,在△ABC中,∠ACB=90°,点D是AB的中点,点E在AC上,点E、D、F一条直线上,且ED=FD,