题目内容
若一元二次方程ax2+bx+c=0的两个根是-3和1，那么二次函数y=ax2+bx+c与x轴的交点是 ．
考点：抛物线与x轴的交点
专题：
分析：利用y=0时求出方程的根即为二次函数图象与x轴交点横坐标，进而得出答案．
解答：解：∵一元二次方程ax2+bx+c=0的两个根是-3和1，
∴二次函数y=ax2+bx+c与x轴的交点是：（-3，0）、（1，0）．
故答案为：（-3，0）、（1，0）．
∴二次函数y=ax2+bx+c与x轴的交点是：（-3，0）、（1，0）．
故答案为：（-3，0）、（1，0）．
点评：此题主要考查了抛物线与x轴的交点，根据二次函数图象与x轴交点求法得出是解题关键．
练习册系列答案
相关题目
如图，上午8时一条船从A出发（60海里/时）向正东航行，8时30分到B处，经测小岛M在A北偏东45°，在B北偏东30°方向，那么BM的距离为（ ）A、20（
| ||
B、30
| ||
C、15（
| ||
D、30（
|
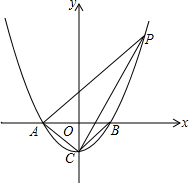如图，已知抛物线y=x2-1与x轴交于A、B两点，与y轴交于点C
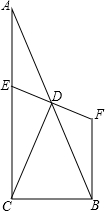如图，在△ABC中，∠ACB=90°，点D是AB的中点，点E在AC上，点E、D、F一条直线上，且ED=FD，下列各组中的两个项不属于同类项的是（ ）
| A、3x2y和-2x2y | ||
| B、-xy和2yx | ||
C、-1和1
| ||
| D、a2b和ab2 |