题目内容
10. 如图,在⊙O中,弦AB=8,M是弦AB上的动点,且OM的最小值为3.则⊙O的半径为5.
如图,在⊙O中,弦AB=8,M是弦AB上的动点,且OM的最小值为3.则⊙O的半径为5.
分析 根据垂线段最短知,当OM⊥AB时,OM有最小值.根据垂径定理和勾股定理求解.
解答  解:根据垂线段最短知,当OM⊥AB时,OM有最小值,
解:根据垂线段最短知,当OM⊥AB时,OM有最小值,
此时,由垂径定理知,点M是AB的中点,
连接OA,AM=$\frac{1}{2}$AB=4,
由勾股定理知,OA2=OM2+AM2.
即OA2=42+32,
解得OA=5.
所以⊙O的半径为5;
故答案为5.
点评 本题考查了垂径定理和勾股定理,根据垂线段最短知,当OM⊥AB时,OM有最小值是解题的关键.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
20.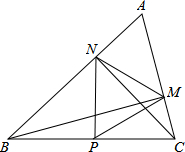 如图,在△ABC中∠A=60°,BM⊥AC于点M,CN⊥AB于点N,P为BC边的中点,连接PM,PN,则下列结论:①PM=PN;②△PMN为等边三角形;下面判断正确是( )
如图,在△ABC中∠A=60°,BM⊥AC于点M,CN⊥AB于点N,P为BC边的中点,连接PM,PN,则下列结论:①PM=PN;②△PMN为等边三角形;下面判断正确是( )
 如图,在△ABC中∠A=60°,BM⊥AC于点M,CN⊥AB于点N,P为BC边的中点,连接PM,PN,则下列结论:①PM=PN;②△PMN为等边三角形;下面判断正确是( )
如图,在△ABC中∠A=60°,BM⊥AC于点M,CN⊥AB于点N,P为BC边的中点,连接PM,PN,则下列结论:①PM=PN;②△PMN为等边三角形;下面判断正确是( )| A. | ①正确 | B. | ②正确 | C. | ①②都正确 | D. | ①②都不正确 |
18. 如图,钟表上显示的时间是12:20,此时,时针与分针的夹角是( )
如图,钟表上显示的时间是12:20,此时,时针与分针的夹角是( )
 如图,钟表上显示的时间是12:20,此时,时针与分针的夹角是( )
如图,钟表上显示的时间是12:20,此时,时针与分针的夹角是( )| A. | 100° | B. | 110° | C. | 115° | D. | 120° |
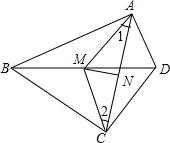 如图,在四边形ABCD中,∠BAD=∠BCD=90°,M、N分别是BD、AC的中点
如图,在四边形ABCD中,∠BAD=∠BCD=90°,M、N分别是BD、AC的中点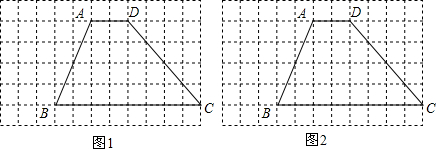
 如图,AB为⊙O的直径,CE是⊙O的切线,且AE⊥CE,垂足为E,BC的延长线交AE的延长线于点D.
如图,AB为⊙O的直径,CE是⊙O的切线,且AE⊥CE,垂足为E,BC的延长线交AE的延长线于点D. 已知AB=10cm,BC=4cm.
已知AB=10cm,BC=4cm.