题目内容
1.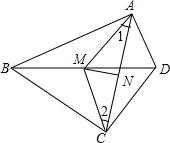 如图,在四边形ABCD中,∠BAD=∠BCD=90°,M、N分别是BD、AC的中点
如图,在四边形ABCD中,∠BAD=∠BCD=90°,M、N分别是BD、AC的中点(1)求证:MN⊥AC;
(2)若∠ADC=120°,求∠1的度数.
分析 (1)首先由直接三角形的斜边上的中线的性质得出AM=CM,进一步利用等腰三角形的三线合一得出结论;
(2)由直接三角形的斜边上的中线的性质得出AM=MD=MC,利用三角形的内角和得出∠AMD=180°-2∠ADM,∠CMD=180°-2∠CDM,求得∠AMC,进一步利用等腰三角形的性质得出答案即可.
解答 (1)证明:∵∠BAD=∠BCD=90°,M是BD的中点,
∴AM=$\frac{1}{2}$BD,CM=$\frac{1}{2}$BD,
∵N是AC的中点,
∴MN⊥AC;
(2)解:∵M是BD的中点,
∴MD=$\frac{1}{2}$BD,
∴AM=DM,
∴∠AMD=180°-2∠ADM,
同理∠CMD=180°-2∠CDM,
∴∠AMC=∠AMD+∠CMD=180°-2∠ADM+180°-2∠CDM=120°,
∵AM=DM,
∴∠1=∠2=30°.
点评 本题考查了直角三角形斜边上中线性质,等腰三角形的判定的应用与性质,三角形的内角和定理,掌握图形的基本性质是解决问题的关键.

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
11.下列各对数中,互为相反数的是( )
| A. | 2和$\frac{1}{2}$ | B. | $\frac{2}{5}$和-0.4 | C. | $\frac{2}{5}$和-$\frac{5}{2}$ | D. | 2和-$\frac{1}{2}$ |
12.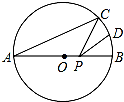 如图,AB是⊙O的直径,AB=2,点C在⊙O上,∠CAB=30°,D为弧BC的中点,P是直径AB上一动点,则PC+PD的最小值为( )
如图,AB是⊙O的直径,AB=2,点C在⊙O上,∠CAB=30°,D为弧BC的中点,P是直径AB上一动点,则PC+PD的最小值为( )
 如图,AB是⊙O的直径,AB=2,点C在⊙O上,∠CAB=30°,D为弧BC的中点,P是直径AB上一动点,则PC+PD的最小值为( )
如图,AB是⊙O的直径,AB=2,点C在⊙O上,∠CAB=30°,D为弧BC的中点,P是直径AB上一动点,则PC+PD的最小值为( )| A. | 2$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | 1 | D. | 2 |
9.数据:-2,-1,0,1,2的平均数是( )
| A. | -2 | B. | -1 | C. | 0 | D. | 6 |
13. 如图所示的正六棱柱,不是正六棱柱三视图的是( )
如图所示的正六棱柱,不是正六棱柱三视图的是( )
 如图所示的正六棱柱,不是正六棱柱三视图的是( )
如图所示的正六棱柱,不是正六棱柱三视图的是( )| A. |  | B. |  | C. |  | D. |  |
 如图,方格纸上画有两条线段,请再画1条线段,使图中的3条线段组成一个轴对称图形(找出符合条件的所有线段).
如图,方格纸上画有两条线段,请再画1条线段,使图中的3条线段组成一个轴对称图形(找出符合条件的所有线段). 如图,AB为⊙O的直径,且AB=4,CD是弦,∠BAC=30°,OE⊥AC,垂足为E;CD⊥AB,垂足为F.
如图,AB为⊙O的直径,且AB=4,CD是弦,∠BAC=30°,OE⊥AC,垂足为E;CD⊥AB,垂足为F. 如图,在⊙O中,弦AB=8,M是弦AB上的动点,且OM的最小值为3.则⊙O的半径为5.
如图,在⊙O中,弦AB=8,M是弦AB上的动点,且OM的最小值为3.则⊙O的半径为5.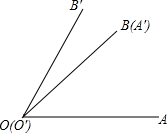 如图,将∠A′O′B′的顶点0′和∠A0B的顶点0重合,边0′A与边0B重合,并使两个角的另一边0A和0′B′分别在重合边0B(O′A)的两旁,这时它们不重合的两边组成∠AOB′.那么∠AOB′,∠A0B与∠A′0′B′之间有什么数量关系?
如图,将∠A′O′B′的顶点0′和∠A0B的顶点0重合,边0′A与边0B重合,并使两个角的另一边0A和0′B′分别在重合边0B(O′A)的两旁,这时它们不重合的两边组成∠AOB′.那么∠AOB′,∠A0B与∠A′0′B′之间有什么数量关系?