题目内容
已知:点O到△ABC的两边AB、AC所在直线的距离相等,且OB=OC.
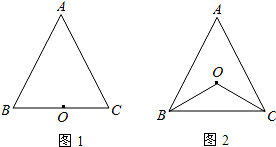
(1)如图1,若点O在BC上,求证:∠ABC=∠ACB;
(2)如图2,若点O在△ABC内部,∠OBC=∠OCB,求证:∠ABC=∠ACB;
(3)猜想,若O点在△ABC的外部,∠ABC=∠ACB成立吗?请画图表示.

(1)如图1,若点O在BC上,求证:∠ABC=∠ACB;
(2)如图2,若点O在△ABC内部,∠OBC=∠OCB,求证:∠ABC=∠ACB;
(3)猜想,若O点在△ABC的外部,∠ABC=∠ACB成立吗?请画图表示.
考点:角平分线的性质,全等三角形的判定与性质
专题:
分析:(1)根据HL证Rt△OEB≌Rt△OFC,根据全等三角形的性质得出∠ABC=∠ACB,即可得出答案;
(2)根据HL证Rt△OEB≌Rt△OFC,根据全等三角形的性质得出∠EBO=∠FCO,即可得出答案;
(3)画出符合条件的两种情况:图③和图④,根据HL证Rt△OEB≌Rt△OFC,根据全等三角形的性质得出∠EBO=∠FCO,即可得出答案.
(2)根据HL证Rt△OEB≌Rt△OFC,根据全等三角形的性质得出∠EBO=∠FCO,即可得出答案;
(3)画出符合条件的两种情况:图③和图④,根据HL证Rt△OEB≌Rt△OFC,根据全等三角形的性质得出∠EBO=∠FCO,即可得出答案.
解答:(1)证明:如图1,
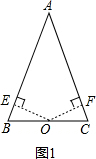
过O作OE⊥AB于E,OF⊥AC于F,
则∠OEB=∠OFC=90°,
∵点O到△ABC的两边AB、AC所在直线的距离相等,
∴OE=OF,
在Rt△OEB和Rt△OFC中,
,
∴Rt△OEB≌Rt△OFC(HL),
∴∠ABC=∠ACB;
(2)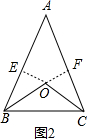
证明:如图2,过O作OE⊥AB于E,OF⊥AC于F,
则∠OEB=∠OFC=90°,
∵点O到△ABC的两边AB、AC所在直线的距离相等,
∴OE=OF,
在Rt△OEB和Rt△OFC中
∴Rt△OEB≌Rt△OFC(HL),
∴∠ABO=∠ACO,
∵∠OBC=∠OCB,
∴∠ABC=∠ACB;
(3)解:若O点在△ABC的外部,∠ABC=∠ACB不一定成立,
理由是:①当∠A的平分线和BC的垂直平分线重合时,如图3,
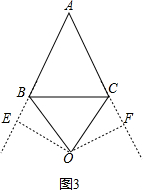
过O作OE⊥AB交AB的延长线于E,OF⊥AC交AC的延长线于F,
则∠OEB=∠OFC=90°,
∵点O到△ABC的两边AB、AC所在直线的距离相等,
∴OE=OF,
在Rt△OEB和Rt△OFC中
∴Rt△OEB≌Rt△OFC(HL),
∴∠EBO=∠FCO,
∵OB=OC,
∴∠OBC=∠OCB,
∵∠ABC=180°-(∠OBC+∠EBO),∠ACB=180°-(∠OCB+∠FCO),
∴∠ABC=∠ACB;
②当∠A的平分线和BC的垂直平分线不重合时,如图④,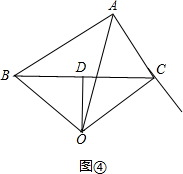
此时∠ABC和∠ACB不相等.

过O作OE⊥AB于E,OF⊥AC于F,
则∠OEB=∠OFC=90°,
∵点O到△ABC的两边AB、AC所在直线的距离相等,
∴OE=OF,
在Rt△OEB和Rt△OFC中,
|
∴Rt△OEB≌Rt△OFC(HL),
∴∠ABC=∠ACB;
(2)

证明:如图2,过O作OE⊥AB于E,OF⊥AC于F,
则∠OEB=∠OFC=90°,
∵点O到△ABC的两边AB、AC所在直线的距离相等,
∴OE=OF,
在Rt△OEB和Rt△OFC中
|
∴Rt△OEB≌Rt△OFC(HL),
∴∠ABO=∠ACO,
∵∠OBC=∠OCB,
∴∠ABC=∠ACB;
(3)解:若O点在△ABC的外部,∠ABC=∠ACB不一定成立,
理由是:①当∠A的平分线和BC的垂直平分线重合时,如图3,

过O作OE⊥AB交AB的延长线于E,OF⊥AC交AC的延长线于F,
则∠OEB=∠OFC=90°,
∵点O到△ABC的两边AB、AC所在直线的距离相等,
∴OE=OF,
在Rt△OEB和Rt△OFC中
|
∴Rt△OEB≌Rt△OFC(HL),
∴∠EBO=∠FCO,
∵OB=OC,
∴∠OBC=∠OCB,
∵∠ABC=180°-(∠OBC+∠EBO),∠ACB=180°-(∠OCB+∠FCO),
∴∠ABC=∠ACB;
②当∠A的平分线和BC的垂直平分线不重合时,如图④,

此时∠ABC和∠ACB不相等.
点评:本题考查了等腰三角形的性质,全等三角形的性质和判定应用,解此题的关键是求出Rt△OEB≌Rt△OFC,题目比较好,证明过程类似.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
三角形三边上的高分别是3、4、5,则这个三角形是( )
| A、锐角三角形 | B、直角三角形 |
| C、钝角三角形 | D、不能确定 |
等腰三角形两边长分别为5和7,则它的周长是( )
| A、19 | B、11 |
| C、17 | D、17或19 |
如果a<0,b>0,a+b<0,那么下列各式中大小关系正确的是( )
| A、a<-b<b<-a |
| B、a<-b<-a<b |
| C、-b<a<b<-a |
| D、-b<a<-a<b |
 在Rt△ABC中,∠C=90°,AC=1,BC=
在Rt△ABC中,∠C=90°,AC=1,BC= 如图,已知Rt△ABC是⊙O的内接三角形,其中直角边AC=8,BC=6,则⊙O的半径是
如图,已知Rt△ABC是⊙O的内接三角形,其中直角边AC=8,BC=6,则⊙O的半径是