题目内容
14．从-1，0，$\frac{22}{7}$，$\sqrt{2}$，$\root{3}{8}$中任取一个数，则取到的数是无理数的概率是$\frac{1}{5}$．分析 先找出无理数的个数，再根据概率公式即可得出答案．
解答 解：∵在-1，0，$\frac{22}{7}$，$\sqrt{2}$，$\root{3}{8}$中，无理数有$\sqrt{2}$，共1个，
∴取到的数是无理数的概率是$\frac{1}{5}$；
故答案为：$\frac{1}{5}$．
点评 此题考查了概率公式和无理数的定义，找出无理数的个数是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
4．点P（-a，b）关于y轴对称的点P′的坐标为（ ）
| A． | （a，b） | B． | （a，-b） | C． | （-a，b） | D． | （-a，-b） |
19．下列命题正确的是（ ）
| A． | a=$\sqrt{{a}^{2}}$=（$\sqrt{a}$）2 | B． | 若$\sqrt{{a}^{2}}$=a，则a=（$\sqrt{a}$）2 | C． | （2$\sqrt{-7}$）2=28 | D． | 2$\sqrt{（-4）^{2}}$=-8 |
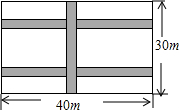张明的父亲打算在院子里种上蔬菜．已知院子是东西长为40m，南北宽为30m的长方形，为了行走方便，要修筑同样宽的三条道路（如图），东西方向两条，南北方向一条．南北方道路垂直于东西道路，余下的部分分别种上蔬菜．若每条道路的宽为1m，求种蔬菜的土地的总面积．