题目内容
如图，在?ABCD中，对角线AC，BD相交于点O，若DO=1.5cm，AB=5cm，BC=4cm，求?ABCD的面积．考点：平行四边形的性质
专题：
分析：由四边形ABCD是平行四边形，可得BD=2DO=2×1.5=3（cm），CD=AB=5cm，又由BC=4cm，可得△BCD是直角三角形，继而求得?ABCD的面积．
解答：解：∵四边形ABCD是平行四边形，
∴BD=2DO=2×1.5=3（cm），CD=AB=5cm，
∵BC=4cm，
∴BC2+BD2=CD2，
∴∠CBD=90°，
即DB⊥BC，
∴S?ABCD=BC•BD=4×3=12（cm2）．
∴BD=2DO=2×1.5=3（cm），CD=AB=5cm，
∵BC=4cm，
∴BC2+BD2=CD2，
∴∠CBD=90°，
即DB⊥BC，
∴S?ABCD=BC•BD=4×3=12（cm2）．
点评：此题考查了平行四边形的性质以及勾股定理的逆定理．此题难度适中，注意掌握数形结合思想的应用．
练习册系列答案
相关题目
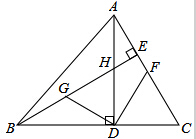如图，△ABC中，AD、BE分别是BC、AC边上的高，且交于H，G为BH的中点，F为AC中点，且∠ABC=45°，求证：DG=DF，DG⊥DF．