题目内容
16.某人计划20天内至少加工400个零件,前5天平均每天加工了33个零件,此后,该工人平均每天至少需加工多少个零件,才能在规定的时间内完成任务?分析 设以后平均每天至少加工x个零件,根据20天内至少加工400个零件,可得不等式,解出即可.
解答 解:设以后平均每天至少加工x个零件,
由题意得:5×33+(20-5)x≥400,
解得:x≥15$\frac{2}{3}$.
∵x为正整数,
∴x取16.
答:该工人以后平均每天至少加工16个零件.
点评 本题考查了一元一次不等式的应用,解答本题的关键是仔细审题,找到不等关系,得出不等式,难度一般.

练习册系列答案
相关题目
6.$\sqrt{4}$的算术平方根是( )
| A. | 4 | B. | 2 | C. | $\sqrt{2}$ | D. | ±2 |
8.下列各题的计算,正确的是( )
| A. | (a2)2=a4 | B. | (-3a2)2=-9a4 | C. | (-a)•(-a)4=a5 | D. | a2+a2=2a4 |
5.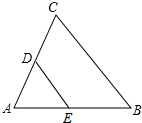 如图,在△ABC中,D、E分别是边AC、AB上的点,下列命题中,假命题是( )
如图,在△ABC中,D、E分别是边AC、AB上的点,下列命题中,假命题是( )
 如图,在△ABC中,D、E分别是边AC、AB上的点,下列命题中,假命题是( )
如图,在△ABC中,D、E分别是边AC、AB上的点,下列命题中,假命题是( )| A. | 若$\frac{AD}{AC}$=$\frac{DE}{BC}$,则△ADE与△ABC相似 | B. | 若$\frac{AD}{DC}$=$\frac{AE}{EB}$,则△ADE与△ABC相似 | ||
| C. | 若$\frac{AD}{AB}$=$\frac{AE}{AC}$,则△ADE与△ABC相似 | D. | 若∠ADE=∠B,则△ADE与△ABC相似 |

 如图,在△ABC中,∠BCA=90°,以BC为直径的⊙O交AB于点P,Q是AC的中点,连接QP并延长交CB的延长线于点D.
如图,在△ABC中,∠BCA=90°,以BC为直径的⊙O交AB于点P,Q是AC的中点,连接QP并延长交CB的延长线于点D.