题目内容
计算
(1)计算:2cos30°+(
-2)-1+|-
|
(2)解方程:
-
=0.
(1)计算:2cos30°+(
| 3 |
| 1 |
| 2 |
(2)解方程:
| 3 |
| x2+2x |
| 1 |
| x2-2x |
考点:二次根式的混合运算,负整数指数幂,解分式方程,特殊角的三角函数值
专题:计算题
分析:(1)根据特殊角的三角函数、负指数幂运算、绝对值进行计算即可;
(2)先去分母,化为整式方程求解即可.
(2)先去分母,化为整式方程求解即可.
解答:解:(1)原式=2×
+
+
=
-(
+2)+
=-
;
(2)去分母,得3x2-6x-x2-2x=0,
解得x1=0,x2=4,
经检验:x=0是增根,
故x=4是原方程的解.
| ||
| 2 |
| 1 | ||
|
| 1 |
| 2 |
=
| 3 |
| 3 |
| 1 |
| 2 |
=-
| 3 |
| 2 |
(2)去分母,得3x2-6x-x2-2x=0,
解得x1=0,x2=4,
经检验:x=0是增根,
故x=4是原方程的解.
点评:本题考查了二次根式的混合运算、负指数幂运算、解分式方程以及特殊角的三角函数值,是基础知识要熟练掌握.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
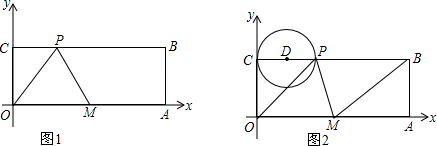
 如图,已知抛物线y=
如图,已知抛物线y=
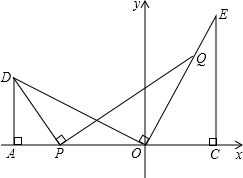 如图,坐标原点O在线段AC上,点D,E在AC同侧,∠DAC=∠ECA=90°,OD⊥OE,AD=OC=3,CE=6,点P为线段AO上的动点,连接DP,作PQ⊥DP,交直线OE与点Q;
如图,坐标原点O在线段AC上,点D,E在AC同侧,∠DAC=∠ECA=90°,OD⊥OE,AD=OC=3,CE=6,点P为线段AO上的动点,连接DP,作PQ⊥DP,交直线OE与点Q;