题目内容
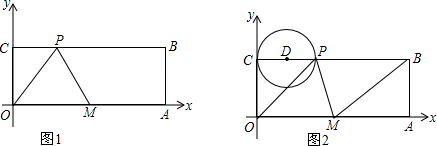
如图,在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A、C的坐标分别为A(8,0),C(0,3),M是OA的中点,动点P从点C出发,沿着在CB以2个单位长度/秒的速度匀速向点B运动,达到点B后停止,连接OP,PM.
(1)点P的坐标为 ;(用含有r的代数式表示)
(2)求当t为何值时,△OPM是以PM为腰的等腰三角形?
(3)如图2,以PC为直径作⊙D,连接BM,试求t为何值时,⊙D与BM相切?并直接写出⊙D与线段BM有两个交点时,t的取值范围.
(1)点P的坐标为
(2)求当t为何值时,△OPM是以PM为腰的等腰三角形?
(3)如图2,以PC为直径作⊙D,连接BM,试求t为何值时,⊙D与BM相切?并直接写出⊙D与线段BM有两个交点时,t的取值范围.

考点:圆的综合题
专题:
分析:(1)根据点的移动规律,求出P点坐标;
(2)分两种情况讨论:①当PM=OP时,则点P在OM的垂直平分线上;②当PM=OM时,过点P作PF⊥OA于点F,再分两种情况讨论:当点F在点M左侧时;当点F在点M右侧时.
(3)当⊙D与BM相切时,设切点为E,根据△BDE∽△MBA列出比例式,求出t的值.
(2)分两种情况讨论:①当PM=OP时,则点P在OM的垂直平分线上;②当PM=OM时,过点P作PF⊥OA于点F,再分两种情况讨论:当点F在点M左侧时;当点F在点M右侧时.
(3)当⊙D与BM相切时,设切点为E,根据△BDE∽△MBA列出比例式,求出t的值.
解答:解:(1)P点坐标为(2t,3).
(2)∵四边形OABC是矩形,点A、C的坐标分别为A(8,0),C(0,3),
∴OC=3,OA=8,
∵M点为OA中点,
∴OM=AM=4,
①当PM=OP时,则点P在OM的垂直平分线上,
∴PC=2,t=1;
②当PM=OM时,如图1,过点P作PF⊥OA于点F,则易得,PF=OC=3,

∴FM=
=
.
当点F在点M左侧时,有PC=OF=4-
,∴t=
.
当点F在点M右侧时,有PC=OF=4+
,∴t=
.
∴当t=1或t=
或t=
时,△OPM是以PM为腰的等腰三角形.
(3)如图2,当⊙D与BM相切时,设切点为E,连接DE,则DE⊥BE,∠DEB=90°,

∵PC=2t,∴CD=DP=DE=t,BD=8-t.
∵四边形OABC是矩形,
∴OA∥BC,∠OAB=90°,
∴∠AMB=∠CBM,且在直角Rt△ABM中,易得BM=5,
∴△BDE∽△MBA,
∴
=
,即
=
,
∴t=3,
∴当t=3时,⊙D与BM相切,
⊙D与线段BM有两个交点时,t的取值范围是3<t≤
.
故答案为(2t,3).
(2)∵四边形OABC是矩形,点A、C的坐标分别为A(8,0),C(0,3),
∴OC=3,OA=8,
∵M点为OA中点,
∴OM=AM=4,
①当PM=OP时,则点P在OM的垂直平分线上,
∴PC=2,t=1;
②当PM=OM时,如图1,过点P作PF⊥OA于点F,则易得,PF=OC=3,

∴FM=
| 42-32 |
| 7 |
当点F在点M左侧时,有PC=OF=4-
| 7 |
4-
| ||
| 2 |
当点F在点M右侧时,有PC=OF=4+
| 7 |
4+
| ||
| 2 |
∴当t=1或t=
4-
| ||
| 2 |
4+
| ||
| 2 |
(3)如图2,当⊙D与BM相切时,设切点为E,连接DE,则DE⊥BE,∠DEB=90°,

∵PC=2t,∴CD=DP=DE=t,BD=8-t.
∵四边形OABC是矩形,
∴OA∥BC,∠OAB=90°,
∴∠AMB=∠CBM,且在直角Rt△ABM中,易得BM=5,
∴△BDE∽△MBA,
∴
| DE |
| AB |
| BD |
| BM |
| t |
| 3 |
| 8-t |
| 5 |
∴t=3,
∴当t=3时,⊙D与BM相切,
⊙D与线段BM有两个交点时,t的取值范围是3<t≤
| 25 |
| 8 |
故答案为(2t,3).
点评:本题考查了圆综合题,涉及动点问题和三角形相似及等腰三角形的性质及矩形的性质,要注意进行分类讨论.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,可以自由转动的转盘被3等分,指针落在每个扇形内的机会均等.
如图所示,可以自由转动的转盘被3等分,指针落在每个扇形内的机会均等.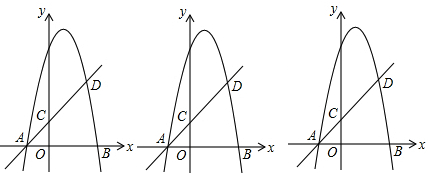
 如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,这时,海轮所在的B处距离灯塔P有多远?(结果用非特殊角的三角函数及根式表示即可)
如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,这时,海轮所在的B处距离灯塔P有多远?(结果用非特殊角的三角函数及根式表示即可)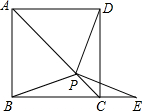 如图,在正方形ABCD中,P是对角线AC上的一点,连接BP、DP,延长BC到E,使PB=PE.求证:∠PDC=∠PEC.
如图,在正方形ABCD中,P是对角线AC上的一点,连接BP、DP,延长BC到E,使PB=PE.求证:∠PDC=∠PEC. 如图,直线a、b与直线c相交,且a∥b,∠α=55°,则∠β=
如图,直线a、b与直线c相交,且a∥b,∠α=55°,则∠β=