题目内容
7.如图1,已知AC是矩形纸片ABCD的对角线,AB=3,∠ACB=30°,现将矩形ABCD沿对角线AC剪开,再把△ABC沿着AD方向平移,得到图2中A′B′C′,当四边形A′ECF是菱形时,平移距离AA′的长是( )
| A. | $\sqrt{3}$ | B. | $\frac{3\sqrt{3}}{2}$ | C. | 2$\sqrt{3}$ | D. | $\frac{9}{2}$ |
分析 由∠A=30°,A′B=DC=3,可得AD=3$\sqrt{3}$,通过特殊角30°的函数值,把线段A′E、A′F用AA′的代数式表示出来,由A′E=A′F,可求出AA′的值.
解答 解:如图(2)设AA′=x,
∵∠A=30°,A′B=DC=3,
∴AD=3$\sqrt{3}$,
∴A′D=3$\sqrt{3}$-x,A′E=$\frac{x}{\sqrt{3}}$
∵四边形A′ECF是菱形
∴A′E∥FC,A′E=A′F,
∴∠DA′F=∠A=30°,
∴A′F=$\frac{A′D}{cos30°}$=$\frac{6\sqrt{3}-2x}{\sqrt{3}}$,
∴$\frac{x}{\sqrt{3}}$=$\frac{6\sqrt{3}-2x}{\sqrt{3}}$,
∴x=2$\sqrt{3}$
故选C.
点评 本题主要考查了三角函数、矩菱形的性质,正确辅助未知数,构建方程是解决问题的关键.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
18.世界上最小的开花结果植物是澳大利亚的出水浮萍,这种植物的果实像一个微笑的无花果,质量只有0.000000076克,将0.000000076克用科学记数法表示为( )
| A. | 7.6×10-8 | B. | 0.76×10-9 | C. | 7.6×108 | D. | 0.76×109 |
 如图,在△ABC中,AB=4,AC=3,AD、AE分别是其角平分线和中线,过点C作CG⊥AD于F,交AB于G,连接EF,则线段EF的长为$\frac{1}{2}$.
如图,在△ABC中,AB=4,AC=3,AD、AE分别是其角平分线和中线,过点C作CG⊥AD于F,交AB于G,连接EF,则线段EF的长为$\frac{1}{2}$. 已知二次函数y=ax2+bx+c的图象过点(1,0),(-3,0),(0,$\frac{3}{2}$).
已知二次函数y=ax2+bx+c的图象过点(1,0),(-3,0),(0,$\frac{3}{2}$).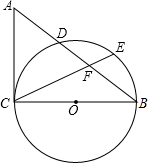 如图,在△ABC中,以BC为直径的⊙O与边AB交于点D,E为的中点,连结CE交AB于点F,AF=AC.
如图,在△ABC中,以BC为直径的⊙O与边AB交于点D,E为的中点,连结CE交AB于点F,AF=AC.