题目内容
11.(1)计算:①$\sqrt{2}$+|$\sqrt{3}$-$\sqrt{2}$|;②(-2)2-$\sqrt{9}$+$\root{3}{8}$(2)一个数的两个不同平方根分别为a+3与2a-6,求该数.
分析 (1)①首先根据绝对值的含义以及平方根的大小关系,求出|$\sqrt{3}$-$\sqrt{2}$|的值是多少,然后再把它和$\sqrt{2}$求和即可;
②首先根据一个数的平方等于这个数和它本身的乘积,求出(-2)2的值是多少;然后根据平方根的求法,求出$\sqrt{9}$的值;再根据立方根的求法,求出$\root{3}{8}$的值;最后求和,求出算式的值是多少即可;
(2)根据正数的两个平方根互为相反数,它们的和为0,可得(a+3)+(2a-6)=0,据此求出a的值是多少;然后把a的值代入,求出(a+3)2的值是多少,即可求出该数是多少.
解答 解:(1)①$\sqrt{2}$+|$\sqrt{3}$-$\sqrt{2}$|
=$\sqrt{2}$+$\sqrt{3}$-$\sqrt{2}$
=$\sqrt{2}-\sqrt{2}+\sqrt{3}$
=$\sqrt{3}$
②(-2)2-$\sqrt{9}$+$\root{3}{8}$
=4-3+2
=3
(2)根据题意,可得
(a+3)+(2a-6)=0,
整理,可得3a-3=0,
解得a=1,
所以(a+3)2
=(1+3)2
=42
=16
则该数为16.
点评 此题主要考查了一个数的平方根、立方根的求法,解答此题的关键是要明确:正数的两个平方根互为相反数,它们的和为0.

练习册系列答案
相关题目
6.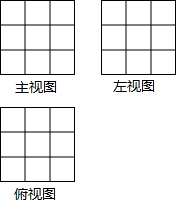 由若干个边长为1的小正方形组成一个空间几何体(小正方形可以悬空),其三视图如图,则这样的小正方体至少应有( )
由若干个边长为1的小正方形组成一个空间几何体(小正方形可以悬空),其三视图如图,则这样的小正方体至少应有( )
 由若干个边长为1的小正方形组成一个空间几何体(小正方形可以悬空),其三视图如图,则这样的小正方体至少应有( )
由若干个边长为1的小正方形组成一个空间几何体(小正方形可以悬空),其三视图如图,则这样的小正方体至少应有( )| A. | 8个 | B. | 10个 | C. | 12个 | D. | 14个 |
1.3的平方根是( )
| A. | 3 | B. | ±3 | C. | $\sqrt{3}$ | D. | ±$\sqrt{3}$ |

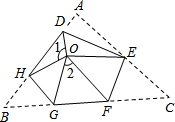 如图,将△ABC三个角分别沿DE、HG、EF翻折,三个顶点均落在点O处,则∠1+∠2的度数为180°.
如图,将△ABC三个角分别沿DE、HG、EF翻折,三个顶点均落在点O处,则∠1+∠2的度数为180°.