题目内容
12. 如图,在△ABC中,AB=AC=10cm,BC=12cm,点P从点C出发,在线段CB上以每秒1cm的速度向点B匀速运动.与此同时,点M从点B出发,在线段BA上以每秒lcm的速度向点A匀速运动.过点P作PN⊥BC,交AC点N,连接MP,MN.当点P到达BC中点时,点P与M同时停止运动.设运动时间为t秒(t>0).
如图,在△ABC中,AB=AC=10cm,BC=12cm,点P从点C出发,在线段CB上以每秒1cm的速度向点B匀速运动.与此同时,点M从点B出发,在线段BA上以每秒lcm的速度向点A匀速运动.过点P作PN⊥BC,交AC点N,连接MP,MN.当点P到达BC中点时,点P与M同时停止运动.设运动时间为t秒(t>0).(1)当t为何值时,PM⊥AB.
(2)设△PMN的面积为y(cm2),求出y与x之间的函致关系式.
(3)是否存在某一时刻t,使S△PMN:S△ABC=1:5?若存在,求出t的值;若不存在,说明理由.
分析 (1)根据△BMP∽△BDA得$\frac{BM}{BD}=\frac{PB}{AB}$即可列出方程解决.
(2)根据△BMP∽△BDA得$\frac{PN}{AD}=\frac{CP}{CD}$求出PN,MF,在证明四边形DPEF是矩形得到ME即可.
(3)代入(2)即可用方程解决.
解答 解:(1)过点A作AD⊥BC于D,
∵AB=AC,∠ADB=90°,
∴BD=CD=6,
∴$AD=\sqrt{A{B}^{2}-C{D}^{2}}$=8,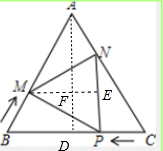
∵MP⊥AB,
∴∠BMP=∠ADB=90°,
∵∠B=∠B,
∴△BMP∽△BDA,
∴$\frac{BM}{BD}=\frac{PB}{AB}$,
∴$\frac{t}{6}=\frac{12-t}{10}$解得t=4.5,
∴当t为4.5时,PM⊥AB
(2)过点M作ME⊥NP于E,交AD于F.
∵BC⊥NP,
∴∠ADC=∠NPC=90°,
∵∠C=∠C,
∴△CPN∽△CDA,
∴$\frac{PN}{AD}=\frac{CP}{CD}$,
∴$\frac{PN}{8}=\frac{t}{6}$,
∴PN=$\frac{4}{3}t$,
由△AMF∽△ABD,可得$\frac{MF}{BD}$=$\frac{AM}{AB}$,即$\frac{MF}{6}$=$\frac{10-t}{10}$,
∴MF=$\frac{3}{5}(10-t)$,
∵∠BPN=∠ADP=∠MEP=90°,
∴四边形DPEF是矩形,
∴EF=DP=6-t,
∴ME=MF+EF=$\frac{3}{5}$(10-t)+6-t=12-$\frac{8}{5}$t,
∴S△MPN=$\frac{1}{2}$PN•ME=$\frac{1}{2}$$•\frac{4}{3}t$(12-$\frac{8}{5}$t)=-$\frac{16}{15}$t2+8t,(0<t≤6),
(3)存在.
由题意:-$\frac{16}{15}$t2+8t=$\frac{1}{5}$×$\frac{1}{2}$×12×8,
解得到t=$\frac{3}{2}$或6.
所以t=$\frac{3}{2}$秒或6秒时,S△PMN:S△ABC=1:5.
点评 本题考查相似三角形的判定和性质,矩形的判定和性质、三角形面积公式等知识,本题的解题方法就是用方程的思想解决问题,把实际问题转化为方程是常用的手段.

 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
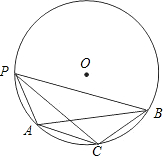 如图,点P为⊙O上一点,弦AB=$\sqrt{3}$cm,PC是∠APB的平分线,∠BAC=30°.
如图,点P为⊙O上一点,弦AB=$\sqrt{3}$cm,PC是∠APB的平分线,∠BAC=30°. 如图,直线l1与直线l2倍直线l3所截,如果同位角∠1与∠3相等,那么内错角∠2与∠4相等,同旁内角∠2与∠3互补.请说明理由.
如图,直线l1与直线l2倍直线l3所截,如果同位角∠1与∠3相等,那么内错角∠2与∠4相等,同旁内角∠2与∠3互补.请说明理由.