题目内容
11. 如图,AB是⊙O的直径,AC是⊙O的切线,BC与⊙O相交于D,连接AD、OD(AC≠AB),则能够判断图中∠B的余角(不再添加任何辅助线)的有( )
如图,AB是⊙O的直径,AC是⊙O的切线,BC与⊙O相交于D,连接AD、OD(AC≠AB),则能够判断图中∠B的余角(不再添加任何辅助线)的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据切线的性质得到AC⊥AB,∠B+∠BAD=90°,于是得到∠B+∠C=90°,根据等腰三角形的性质得到∠B=∠BDO,∠ODA=∠OAD,得到∠B+∠ODA=90°,即可得到结论.
解答 证明:∵AB是⊙O的直径,AC是⊙O的切线,
∴AC⊥AB,∠B+∠BAD=90°,
∴∠B+∠C=90°,
∵OA=OB=OD,
∴∠B=∠BDO,∠ODA=∠OAD,
∴∠B+∠ODA=90°,
∴图中∠B的余角有∠C,∠DAB,∠ODA,
故选C.
点评 本题考查了切线的性质,等腰三角形的性质,熟练掌握切线的性质定理是解题的关键

练习册系列答案
相关题目
9.AB是⊙O的弦,∠AOB=88°,则弦AB所对的圆周角等于( )
| A. | 44° | B. | 22° | C. | 44°或136° | D. | 22°或68° |
6. 如图,在一次数学课外实践活动中,小文在点C处测得树的顶端A的仰角为37°,BC=20m,则树的高度AB为( )
如图,在一次数学课外实践活动中,小文在点C处测得树的顶端A的仰角为37°,BC=20m,则树的高度AB为( )
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
 如图,在一次数学课外实践活动中,小文在点C处测得树的顶端A的仰角为37°,BC=20m,则树的高度AB为( )
如图,在一次数学课外实践活动中,小文在点C处测得树的顶端A的仰角为37°,BC=20m,则树的高度AB为( )(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
| A. | 20m | B. | 15m | C. | 12m | D. | 16m |
16.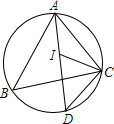 在△ABC中,∠ABC=60°,∠ACB=50°,如图所示,I是△ABC的内心,延长AI交△ABC的外接圆D,则∠ICD的度数是( )
在△ABC中,∠ABC=60°,∠ACB=50°,如图所示,I是△ABC的内心,延长AI交△ABC的外接圆D,则∠ICD的度数是( )
 在△ABC中,∠ABC=60°,∠ACB=50°,如图所示,I是△ABC的内心,延长AI交△ABC的外接圆D,则∠ICD的度数是( )
在△ABC中,∠ABC=60°,∠ACB=50°,如图所示,I是△ABC的内心,延长AI交△ABC的外接圆D,则∠ICD的度数是( )| A. | 50° | B. | 55° | C. | 60° | D. | 65° |
3. 从如图所示的四个带圆圈的数字中,任取两个数字(既可以是相邻也可以是相对的两个数字)相互交换它们的位置,交换一次后能使①、②两数在相对位置上的概率是( )
从如图所示的四个带圆圈的数字中,任取两个数字(既可以是相邻也可以是相对的两个数字)相互交换它们的位置,交换一次后能使①、②两数在相对位置上的概率是( )
 从如图所示的四个带圆圈的数字中,任取两个数字(既可以是相邻也可以是相对的两个数字)相互交换它们的位置,交换一次后能使①、②两数在相对位置上的概率是( )
从如图所示的四个带圆圈的数字中,任取两个数字(既可以是相邻也可以是相对的两个数字)相互交换它们的位置,交换一次后能使①、②两数在相对位置上的概率是( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
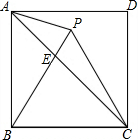 如图,点P在正方形ABCD内,△PBC是正三角形,AC与PB相交于点E.有以下结论:
如图,点P在正方形ABCD内,△PBC是正三角形,AC与PB相交于点E.有以下结论: