AB是⊙O的弦.∠AOB=88°.则弦AB所对的圆周角等于( )A．44°B．22°C．44°或136°D．22°或68° 题目和参考答案——青夏教育精英家教网—

题目内容

9．AB是⊙O的弦，∠AOB=88°，则弦AB所对的圆周角等于（　　）

A．

44°

B．

22°

C．

44°或136°

D．

22°或68°

分析首先根据题意画出图形，然后由圆周角定理求得∠ACB的度数，由圆的内接四边形的性质求得∠ADB的度数，继而可求得答案．

解答解：如图，∵∠AOB=88°，
∴∠ACB=$\frac{1}{2}$∠AOB=44°，
∴∠ADB=180°-∠ACB=136°．
∴弦AB所对的圆周角的度数为：44°或136°．
故选C．

点评此题考查了圆周角定理以及圆的内接四边形的性质．此题难度不大，注意弦所对的圆周角是一对，且互补．

练习册系列答案

相关题目

$-\frac{2}{-9}=\frac{2}{9}$

20．某班同学利用假期参加夏令营活动，分成几个小组，若每组7人还余1人；若每组8人还缺少6人．若设该班分成x个小组，可列方程为7x+1=8x-6．

17．

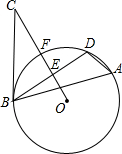如图，△ABD是⊙O的内接三角形，E是弦BD的中点，点C是⊙O外一点且∠DBC=∠A，连接OE延长与圆相交于点F，与BC相交于点C．
（1）求证：BC是⊙O的切线；
（2）若⊙O的半径为6，BC=8，求弦BD的长．

4．

将图中的直角三角板ABC绕AC边旋转一周得到的几何体是圆锥．

14．

小明家住房的结构如图所示（图形均为长方形，单位：米），小明爸爸打算把卧室以外的部分都铺上地板砖，请问
①小明家需要多少平方米的地板砖？如果这种地板砖的价格为a元/平方米，那么购买地板砖至少需要多少元？
②当x=3，y=2.5，a=20时，求小明家购买地板砖需要多少钱？

1．地球上煤的储量大约为15万亿吨，用科学记数法表示为1.5×10¹³吨．

18．如图，已知△ABC≌△A₁B₁C₁，∠A=45°，∠C₁=60°，则∠B=75°．

11．

如图，AB是⊙O的直径，AC是⊙O的切线，BC与⊙O相交于D，连接AD、OD（AC≠AB），则能够判断图中∠B的余角（不再添加任何辅助线）的有（　　）

试题分类