题目内容
14.为了加强对校内外安全监控,创建荔湾平安校园,某学校计划增加15台监控摄像设备,现有甲、乙两种型号的设备,其中每台价格,有效监控半径如表所示,经调查,购买1台甲型设备比购买1台乙型设备多150元,购买2台甲型设备比购买3台乙型设备少400元.| 甲型 | 乙型 | |
| 价格(元/台) | a | b |
| 有效半径(米/台) | 150 | 100 |
(2)若购买该批设备的资金不超过11000元,且两种型号的设备均要至少买一台,学校有哪几种购买方案?
(3)在(2)问的条件下,若要求监控半径覆盖范围不低于1600米,为了节约资金,请你设计一种最省钱的购买方案.
分析 (1)根据购买1台甲型设备比购买1台乙型设备多150元,购买2台甲型设备比购买3台乙型设备少400元,可列出方程组,解之即可得到a、b的值;
(2)可设购买甲型设备x台,则购买乙型设备(15-x)台,根据购买该批设备的资金不超过11000元列不等式,解之确定x的值,即可确定方案;
(3)根据监控半径覆盖范围不低于1600米,列出不等式,根据x的值确定方案,然后对所需资金进行比较,并作出选择.
解答 解:(1)由题意得:
$\left\{\begin{array}{l}{a-b=150}\\{3b-2a=400}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=850}\\{b=700}\end{array}\right.$;
(2)设购买甲型设备x台,则购买乙型设备(15-x)台,依题意得
850x+700(15-x)≤11000,
解得x≤3$\frac{1}{3}$,
∵两种型号的设备均要至少买一台,
∴x=1,2,3,
∴有3种购买方案:①甲型设备1台,乙型设备14台;②甲型设备2台,乙型设备13台;③甲型设备3台,乙型设备12台;
(3)依题意得:150x+100(15-x)≥1600,
解得x≥2,
∴x取值为2或3.
当x=2时,购买所需资金为:850×2+700×13=10800(元),
当x=3时,购买所需资金为:850×3+700×12=10950(元),
∴最省钱的购买方案为:购甲型设备2台,乙型设备13台.
点评 本题考查了一元一次不等式及二元一次方程组的应用,解决本题的关键是读懂题意,找到符合题意的不等关系式及所求量的等量关系.要会用分类的思想来解决讨论方案的问题.

练习册系列答案
相关题目
2.下列计算正确的是( )
| A. | $\sqrt{8}$+$\sqrt{2}$=$\sqrt{10}$ | B. | $\sqrt{8}$-$\sqrt{2}$=$\sqrt{2}$ | C. | $\sqrt{8}×\sqrt{2}$=$\sqrt{16}$ | D. | $\sqrt{8}$÷$\sqrt{2}$=$\sqrt{4}$ |
19.某校八年级部分学生利用课外活动时间,积极参加篮球定点投篮的训练,训练结束后进行一次测试,记录如下表:
回答下列问题:
(1)测试记录中,篮球定点投篮进球数的众数是4个,中位数是5个.
(2)求本次测试的人均进球数.
| 进球数(个) | 8 | 7 | 6 | 5 | 4 | 3 |
| 人数 | 2 | 2 | 5 | 7 | 9 | 3 |
(1)测试记录中,篮球定点投篮进球数的众数是4个,中位数是5个.
(2)求本次测试的人均进球数.
6.已知-1<x<0,那么在x、2x、$\sqrt{(-x)}$、-x2中最小的数是( )
| A. | -x2 | B. | 2x | C. | $\sqrt{(-x)}$ | D. | x |
4.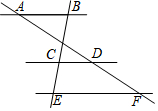 如图,已知AB∥CD∥EF,AD:AF=3:5,BE=15,那么CE的长等于( )
如图,已知AB∥CD∥EF,AD:AF=3:5,BE=15,那么CE的长等于( )
 如图,已知AB∥CD∥EF,AD:AF=3:5,BE=15,那么CE的长等于( )
如图,已知AB∥CD∥EF,AD:AF=3:5,BE=15,那么CE的长等于( )| A. | 9 | B. | 6 | C. | $\frac{15}{2}$ | D. | $\frac{9}{2}$ |
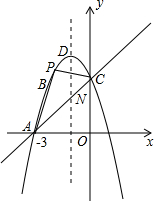 如图,已知抛物线y=ax2+bx+c过点A(-3,0),B(-2,3),C(0,3),其顶点为D.
如图,已知抛物线y=ax2+bx+c过点A(-3,0),B(-2,3),C(0,3),其顶点为D.