题目内容
16.(1)解不等式$\frac{2x+3}{5}$-1≥2(x-1),并写出它的非负整数解.(2)解不等式组$\left\{\begin{array}{l}{\frac{x-3}{2}+3≥x}\\{1-3(x-1)<8-x}\end{array}\right.$.
分析 (1)利用不等式的性质解出不等式的解集,再求其非负整数解;
(2)首先解出不等式组中的x的取值范围,然后找出它们的公共部分,该公共部分就是不等式组的解集.
解答 解:(1)$\frac{2x+3}{5}$-1≥2(x-1),
2x+3-5≥10x-10
-8x≥-8
x≤1
所以其非负整数解为0,1.
(2)$\left\{\begin{array}{l}{\frac{x-3}{2}+3≥x①}\\{1-3(x-1)<8-x②}\end{array}\right.$
解不等式①得x≤3,
解不等式②得x>-2,
所以不等式组的解集为-2<x≤3.
点评 本题考查解不等式与不等式组,求出不等式公共解集,要遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.一个矩形对角线的长为10,两对角线所夹锐角为60°,则这个矩形的周长为( )
| A. | 40 | B. | 20 | C. | 5+5$\sqrt{3}$ | D. | 10+10$\sqrt{3}$ |
8.下列各式因式分解错误的是( )
| A. | 8x2y-24xy2=8xy(x-3y) | B. | ax+bx+ay+by=x(a+b)+y(a+b) | ||
| C. | 12x2y+14x2y2-2xy=2xy(6x+7xy-1) | D. | x2-x-12=(x+3)(x-4) |
6.已知等腰三角形的两边长分别为6厘米和3厘米,则该等腰三角形的周长是( )
| A. | 9厘米 | B. | 12厘米 | C. | 15厘米 | D. | 12厘米或15厘米 |
 已知:如图,BD平分∠ABC,点E在BC上,EF∥AB.若∠CEF=100°,则∠ABD的度数为50°.
已知:如图,BD平分∠ABC,点E在BC上,EF∥AB.若∠CEF=100°,则∠ABD的度数为50°.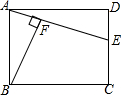 如图,已知E是矩形ABCD的边CD上一点,BF⊥AE于F,试说明:BF•DE=AF•AD.
如图,已知E是矩形ABCD的边CD上一点,BF⊥AE于F,试说明:BF•DE=AF•AD.