题目内容
11．
如图，AB为⊙O的直径，C为⊙O外一点，过点C作⊙O的切线，切点为B，连接AC交⊙O于点D，∠C=40°，点E在AB左侧的半圆上运动（不与A、B重合），则∠AED的大小是（ ）| A． | 20° | B． | 40° | C． | 50° | D． | 80° |
分析 根据切线的性质和圆周角定理得到∠BAD+∠ABD=∠C+∠BAD=90°，再由同角的余角相等得到结论．
解答 
解：连接BD，∵AB为⊙O的直径，
∴∠ADB=90°，
∵BC是⊙O的切线，∴∠ABC=90°，
∴∠BAD+∠ABD=∠C+∠BAD=90°，
∴∠ABD=∠C=40°，
∴∠AED=40°．
故选B．
点评 本题考查了切线的性质，圆周角定理，连接BD是解题的关键．
练习册系列答案
全程金卷系列答案
相关题目
，请你确定一个b的值，使该抛物线与x轴的一个交点在（1，0）和（3，0）之间，你确定的b的值是_______。
如图，长方形ABCD中，AB=DC=6，AD=BC=12动点P从点C出发，沿C--B--C运动，动点Q从点B出发，沿B--A--D--C运动，它们以2厘米/秒速度同时出发，设运动时间为t、△PQC的面积为y，在整个运动过程中，请用t的代数式表示y．
如图，△ABC中，∠A=90°，点D在AC边上，DE∥BC，若∠1=145°，则∠B的度数为50°．
6．
如图，直线a∥b，AB⊥BC，∠1=40°，则∠2的度数为（ ）
如图，直线a∥b，AB⊥BC，∠1=40°，则∠2的度数为（ ）| A． | 30° | B． | 40° | C． | 50° | D． | 60° |
16．某校为了了解学生的体能状况，决定抽取部分同学进行体育测试参加测试的每名学生从“1000米跑步”、“立定跳远”，“1分钟跳绳”、“坐位体前屈”四个项目中随机抽取两项作为测试项目．
（1）求：小明同学恰好抽到“立定跳远”，“坐位体前屈”两项的概率．
（2）据统计，初二三班共10名学生参加了测试，两项的平均成绩如下：
94 100 90 84 92 50 89 64 71 92
①该表是这10名同学平均成绩的一些统计数据，请将表格中缺少的数据补充完整．
②为了调动学生参与体育锻炼的积极性，该班决定对参与测试的同学进行奖励，决定制定一个奖励标准，成绩凡达到或超过这个标准的学生将受到奖励，如果要使参与测试的学生半数左右能获奖，根据上面的计算结果，这个标准应定为多少？并简述理由．
（1）求：小明同学恰好抽到“立定跳远”，“坐位体前屈”两项的概率．
（2）据统计，初二三班共10名学生参加了测试，两项的平均成绩如下：
94 100 90 84 92 50 89 64 71 92
①该表是这10名同学平均成绩的一些统计数据，请将表格中缺少的数据补充完整．
| 平均数 | 中位数 | 众数 |
| 82.6 | 89.5 | 92 |
已知一次函数y=2x-k与反比例函数y=$\frac{k+2}{x}$的图象相交于A、B，其中A的横坐标为3．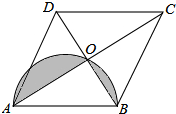
如图，菱形ABCD的对角线AC，BD相交于点O，AC=8，BD=6，以AB为直径作一个半圆，则图中阴影部分的面积为$\frac{25}{8}π-6$．