题目内容
9.某单位今年“十一”期间要组团去北京旅游,与旅行社联系时,甲旅行社提出每人次收300元车费和住宿费,不优惠,乙旅社提出每人次收350元车费和住宿费,但有3人可享受免费待遇(1)分别写出甲、乙两旅行社的收费与旅行人数之间函数关系式.
(2)在同一坐标系内作出它们的图象;
(3)如果组织20人的旅行团,选择哪家旅行社比较合算?当旅行团为多少人时,选甲或乙旅行社所需费用一样多?
(4)由于经费紧张,单位领导计划此次旅行费用不超过5000元,选哪一家旅行社去的人多一些?最多去多少人?
分析 (1)设甲旅行社的收费为y甲元,乙旅行社的收费为y乙元,旅行人数为x人,根据单价乘以数量等于总价就可以表示出y与x之间的函数关系式;
(2)根据(1)中解析式进行描点连线即可画出图象;
(3)将x=20分别代入y甲与y乙的解析式求出y甲与y乙的大小,进行比较就可以求出结论;
(4)将y=5000分别代入两个解析式求出x的值即可求出结论
解答 解:(1)设甲旅行社的收费为y甲元,乙旅行社的收费为y乙元,旅行人数为x人,由题意,得
y甲=300x,
y乙=350(x-3)=350x-1050.
答:y甲=300x,y乙=350x-1050;
(2)如图所示: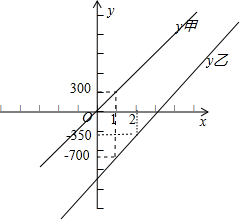
(3)当x=20时,
y甲=300×20=6000元,
y乙=350×20-1050=5950元;
∵6000>5950,
∴y甲>y乙,
∴选择乙旅行社比较合算;
(4)当y=5000时,
5000=300x,
x=$\frac{50}{3}$≈16人;
5000=350x-1050,
x=$\frac{121}{7}$≈17人.
∵16<17.
∴选乙旅行社去的人多些,
最多去的人数:17-16=1人.
答:选乙旅行社去的人多一些,最多去1人.
点评 本题考查了单价×数量=总价的运用,一次函数的解析式的运用,方案设计的运用,解答时求出一次函数的解析式是关键.

练习册系列答案
相关题目
19.下列说法中错误的是( )
| A. | 两条平行线倍第三条直线所截,一对内错角的角平分线互相平行 | |
| B. | 同角的余角相等 | |
| C. | 在同一平面内,不相交的两条线段必平行 | |
| D. | 在同一平面内,若a⊥b,b⊥c,则a∥c |
20.若函数y=$\frac{k}{x}$(k≠0)的图象过点($\frac{1}{2}$,$\frac{4}{3}$),则此函数图象位于( )
| A. | 第一、二象限 | B. | 第一、三象限 | C. | 第二、三象限 | D. | 第二、四象限 |
14. 如图,有三张卡片,它们背面完全相同,现将这三张卡片背面朝上洗均匀后随机抽取一张,以其正面的数字作为a的值,放回后再从中随机抽取一张,以去正面的数字作为b的值,则点(a,b)在第三象限的概率是( )
如图,有三张卡片,它们背面完全相同,现将这三张卡片背面朝上洗均匀后随机抽取一张,以其正面的数字作为a的值,放回后再从中随机抽取一张,以去正面的数字作为b的值,则点(a,b)在第三象限的概率是( )
 如图,有三张卡片,它们背面完全相同,现将这三张卡片背面朝上洗均匀后随机抽取一张,以其正面的数字作为a的值,放回后再从中随机抽取一张,以去正面的数字作为b的值,则点(a,b)在第三象限的概率是( )
如图,有三张卡片,它们背面完全相同,现将这三张卡片背面朝上洗均匀后随机抽取一张,以其正面的数字作为a的值,放回后再从中随机抽取一张,以去正面的数字作为b的值,则点(a,b)在第三象限的概率是( )| A. | $\frac{4}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
1.下列说法中错误的是( )
| A. | 成中心对称的两个图形全等 | |
| B. | 成中心对称的两个图形中,对称点的连线被对称轴平分 | |
| C. | 中心对称图形的对称中心是对称点连线的中心 | |
| D. | 中心对称图形绕对称中心旋转180°后,都能与自身重合 |
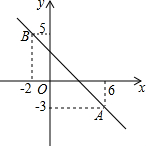 如图,在平面直角坐标系中,一次函数的图象经过点A(6,-3)和点B(-2,5).
如图,在平面直角坐标系中,一次函数的图象经过点A(6,-3)和点B(-2,5).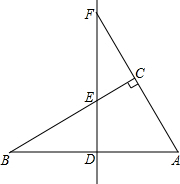 如图,在△ABC中,∠ACB=90°,AB的垂直平分线交AB于点D,交边BC于点E,交边AC的延长线于点F,并且BD=CF.求证:∠CAB=2∠B.
如图,在△ABC中,∠ACB=90°,AB的垂直平分线交AB于点D,交边BC于点E,交边AC的延长线于点F,并且BD=CF.求证:∠CAB=2∠B.