题目内容
2. 如图,矩形ABCD中,线段EF过对角线的交点O,交AB、CD于点E、F,阴影部分的面积为S1,矩形ABCD的面积为S,则$\frac{{S}_{1}}{S}$=$\frac{1}{4}$.
如图,矩形ABCD中,线段EF过对角线的交点O,交AB、CD于点E、F,阴影部分的面积为S1,矩形ABCD的面积为S,则$\frac{{S}_{1}}{S}$=$\frac{1}{4}$.
分析 由四边形ABCD是矩形,推出AB∥CD,OA=OC,OB=OD,推出∠EAO=∠FCO,S△AOB=S△AOD=S△BOC=S△ODC=$\frac{1}{4}$S矩形ABCD,只要证明△AEO≌△CFO,
即可推出S1=S△AOB,由此即可解决问题.
解答 解: ∵四边形ABCD是矩形,
∵四边形ABCD是矩形,
∴AB∥CD,OA=OC,OB=OD,
∴∠EAO=∠FCO,S△AOB=S△AOD=S△BOC=S△ODC=$\frac{1}{4}$S矩形ABCD,
在△AEO和△CFO中,
$\left\{\begin{array}{l}{∠EAO=∠FCO}\\{OA=OC}\\{∠AOE=∠COF}\end{array}\right.$,
∴△AEO≌△CFO(SAS),
∴S1=S△AOB,
∴$\frac{{S}_{1}}{S}$=$\frac{1}{4}$.
故答案为$\frac{1}{4}$.
点评 本题考查矩形的性质、全等三角形的判定和性质、三角形的面积等知识,解题的关键是学会用转化的思想思考问题,本题字母S1=S△AOB是关键,属于中考常考题型.

练习册系列答案
相关题目
13.观察表格中按规律排列的两行数据,若用x,y表示表格中间一列的两个数,则x,y满足的数量关系是x=2+2y.
| 序号 | 1 | 2 | 3 | 4 | 5 | … | … | … |
| 第1行 | 6 | -6 | 18 | -30 | 66 | … | x | … |
| 第2行 | 2 | -4 | 8 | -16 | 32 | … | y | … |
17.下列说法正确的有( )个
①-$\frac{2}{5}$πxy2的系数为-$\frac{2}{5}$;②1是单项式;③$\frac{2}{x}$-5是多项式;④单项式(-2)2x2y3的次数为7.
①-$\frac{2}{5}$πxy2的系数为-$\frac{2}{5}$;②1是单项式;③$\frac{2}{x}$-5是多项式;④单项式(-2)2x2y3的次数为7.
| A. | 3 | B. | 4 | C. | 2 | D. | 1 |
11.肖丽去商店买练习本,回来后告诉同学们:“店主给我说,如果多买一些就给我8折优惠,所以我就买了20本,结果便宜了4.8元.”如果设原来每本练习本价格为x元,则根据题意所列方程错误的是( )
| A. | 20(1-0.8)x=4.8 | B. | 20x-20×0.8x=4.8 | C. | 20x=20×0.8x+4.8 | D. | 20×0.8x=4.8 |
12.矩形ABCD的长AD=15cm,宽AB=10cm,∠ABC的平分线分AD边为AE、ED两部分,这AE、ED的长分别为( )
| A. | 11cm和4cm | B. | 10cm和5cm | C. | 9cm和6cm | D. | 8cm和7cm |
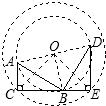 如图,Rt△ABC绕O点旋转90°得Rt△BDE,其中∠ACB=∠E=90°,AC=3,DE=5,则OC的长为4$\sqrt{2}$;若将Rt△ABC绕C点旋转一周,则线段AB扫过的面积是16π(保留π)
如图,Rt△ABC绕O点旋转90°得Rt△BDE,其中∠ACB=∠E=90°,AC=3,DE=5,则OC的长为4$\sqrt{2}$;若将Rt△ABC绕C点旋转一周,则线段AB扫过的面积是16π(保留π) 如图,一艘海轮位于灯塔P的南偏东70°方向的M处,它以40海里/小时的速度向正北方向航行,2小时后到达位于灯塔P的北偏东40°的N处,则N处于灯塔P的距离为80海里.
如图,一艘海轮位于灯塔P的南偏东70°方向的M处,它以40海里/小时的速度向正北方向航行,2小时后到达位于灯塔P的北偏东40°的N处,则N处于灯塔P的距离为80海里.