题目内容
17.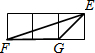 如图,小正方形的边长均为1,则下面4个阴影部分三角形中,能与△EFG相似的是( )
如图,小正方形的边长均为1,则下面4个阴影部分三角形中,能与△EFG相似的是( )| A. | 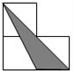 | B. |  | C. | 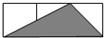 | D. | 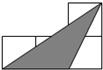 |
分析 根据相似三角形的判定,易得出△ABC的三边的边长,故只需分别求出各选项中三角形的边长,分析两三角形对应边是否成比例即可.
解答 解:∵小正方形的边长为1,
∴在△ABC中,EG=$\sqrt{2}$,FG=2,EF=$\sqrt{1+{3}^{2}}$=$\sqrt{10}$,
A中,一边=1,一边=$\sqrt{5}$,一边=2$\sqrt{2}$,三边与△ABC中的三边不能对应成比例,故两三角形不相似.故A错误;
B中,一边=1,一边=$\sqrt{2}$,一边=$\sqrt{{2}^{2}+1}$=$\sqrt{5}$,有$\frac{\sqrt{2}}{1}$=$\frac{2}{\sqrt{2}}$=$\frac{\sqrt{10}}{\sqrt{5}}$,即三边与△ABC中的三边对应成比例,故两三角形相似.故B正确;
C中,一边=3,一边=$\sqrt{2}$,一边=$\sqrt{1+{2}^{2}}$=$\sqrt{5}$,三边与△ABC中的三边不能对应成比例,故两三角形不相似.故C错误;
D中,一边=2,一边=$\sqrt{5}$,一边=$\sqrt{{3}^{2}+{2}^{2}}$=$\sqrt{13}$,三边与△ABC中的三边不能对应成比例,故两三角形不相似.故D错误.
故选B.
点评 本题考查了相似三角形的判定及勾股定理,识别两三角形相似,除了要掌握定义外,还要注意正确找出两三角形的对应边、对应角,可利用数形结合思想根据图形提供的数据计算对应角的度数、对应边的比.

练习册系列答案
相关题目
8.如果抛物线y=(m-1)x2的开口向上,那么m的取值范围是( )
| A. | m>1 | B. | m≥1 | C. | m<1 | D. | m≤1 |
6.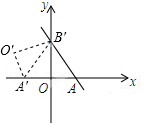 如图,直线y=-$\sqrt{3}$x+4$\sqrt{3}$与x轴、y轴分别交于A、B两点,把△AOB绕点B逆时针旋转,点A在x轴上,得到△A′O′B,则点O′的坐标是( )
如图,直线y=-$\sqrt{3}$x+4$\sqrt{3}$与x轴、y轴分别交于A、B两点,把△AOB绕点B逆时针旋转,点A在x轴上,得到△A′O′B,则点O′的坐标是( )
 如图,直线y=-$\sqrt{3}$x+4$\sqrt{3}$与x轴、y轴分别交于A、B两点,把△AOB绕点B逆时针旋转,点A在x轴上,得到△A′O′B,则点O′的坐标是( )
如图,直线y=-$\sqrt{3}$x+4$\sqrt{3}$与x轴、y轴分别交于A、B两点,把△AOB绕点B逆时针旋转,点A在x轴上,得到△A′O′B,则点O′的坐标是( )| A. | (-2,2$\sqrt{3}$) | B. | (6,2$\sqrt{3}$) | C. | (2,2$\sqrt{3}$) | D. | (-6,2$\sqrt{3}$) |
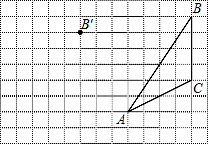 如图,在方格纸内将三角形ABC经过平移后得到三角形A′B′C′,图中标出了点B的对应点B′,解答下列问题.
如图,在方格纸内将三角形ABC经过平移后得到三角形A′B′C′,图中标出了点B的对应点B′,解答下列问题.