题目内容
6.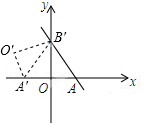 如图,直线y=-$\sqrt{3}$x+4$\sqrt{3}$与x轴、y轴分别交于A、B两点,把△AOB绕点B逆时针旋转,点A在x轴上,得到△A′O′B,则点O′的坐标是( )
如图,直线y=-$\sqrt{3}$x+4$\sqrt{3}$与x轴、y轴分别交于A、B两点,把△AOB绕点B逆时针旋转,点A在x轴上,得到△A′O′B,则点O′的坐标是( )| A. | (-2,2$\sqrt{3}$) | B. | (6,2$\sqrt{3}$) | C. | (2,2$\sqrt{3}$) | D. | (-6,2$\sqrt{3}$) |
分析 过O′作O′C⊥x轴于C,根据一次函数解析式得到A(4,0),B(0,4$\sqrt{3}$),得到OA=4,OB=4$\sqrt{3}$,解直角三角形得到∠BAO=60°,根据旋转的性质得到A′B=AB,A′O′=AO=4,推出△AA′B是等边三角形,求出∠O′A′C=60°,解直角三角形即可得到结论.
解答  解:过O′作O′C⊥x轴于C,
解:过O′作O′C⊥x轴于C,
在y=-$\sqrt{3}$x+4$\sqrt{3}$中,
令x=0,得y=4$\sqrt{3}$,令y=0,得x=4,
∴A(4,0),B(0,4$\sqrt{3}$),
∴OA=4,OB=4$\sqrt{3}$,
∴tan∠BAO=$\frac{OB}{OA}$=$\sqrt{3}$,
∴∠BAO=60°,
∵把△AOB绕点B逆时针旋转,点A在x轴上,得到△A′O′B,
∴A′B=AB,A′O′=AO=4,
∴△AA′B是等边三角形,
∴∠BA′O=∠BA′O′=60°,
∴∠O′A′C=60°,
∴A′C=2,O′C=2$\sqrt{3}$,
∴O′(-6,2$\sqrt{3}$).
点评 本题考查了坐标与图形变换-旋转,等边三角形的判定和性质,解直角三角形,求得∠BAO=60°是解题的关键.

练习册系列答案
相关题目
16.在1,0,-1,-2这四个数中,最小的数是( )
| A. | -1 | B. | -2 | C. | 0 | D. | 1 |
14. 某几何体的三种视图如图所示,则此几何体是( )
某几何体的三种视图如图所示,则此几何体是( )
 某几何体的三种视图如图所示,则此几何体是( )
某几何体的三种视图如图所示,则此几何体是( )| A. | 圆台 | B. | 圆锥 | C. | 圆柱 | D. | 棱柱 |
15.下列等式从左到右的变形是因式分解的是( )
| A. | 6a2b=2a•3ab | B. | (a+3b)(a-3b)=a2-9 | ||
| C. | 4x2+8x-1=4x(x+2)-1 | D. | ax-ay=a(x-y) |
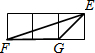 如图,小正方形的边长均为1,则下面4个阴影部分三角形中,能与△EFG相似的是( )
如图,小正方形的边长均为1,则下面4个阴影部分三角形中,能与△EFG相似的是( )

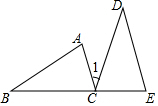 如图,B,C,E三点在同一直线上,AC∥DE,AC=CE=3cm,DE=5cm,∠1=∠B,则BE=8cm.
如图,B,C,E三点在同一直线上,AC∥DE,AC=CE=3cm,DE=5cm,∠1=∠B,则BE=8cm.