题目内容
5.已知点A(2a+3b,-2)与点B(-8,3a+2b)关于坐标原点对称,则a+b=2.分析 直接利用关于原点对称点的性质得出关于a,b的等式进而求出答案.
解答 解:∵点A(2a+3b,-2)与点B(-8,3a+2b)关于坐标原点对称,
∴$\left\{\begin{array}{l}{2a+3b=8}\\{3a+2b=2}\end{array}\right.$,
故5a+5b=10,
则a+b=2.
故答案为:2.
点评 此题主要考查了关于原点对称点的性质,正确记忆横纵坐标的关系是解题关键.

练习册系列答案
相关题目
15.下列命题中:①有公共顶点和一条公共边的两个角一定是邻补角;②垂线段最短;③经过直线外一点,有且只有一条直线与这条直线平行;④相等的角是对顶角;⑤等角的余角相等,其中假命题的个数是( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
16.在1,0,-1,-2这四个数中,最小的数是( )
| A. | -1 | B. | -2 | C. | 0 | D. | 1 |
10.下列计算正确的是( )
| A. | $\sqrt{27}$$÷\sqrt{3}$=3 | B. | 3+$\sqrt{3}$=3$\sqrt{3}$ | C. | $\sqrt{2}+\sqrt{3}$=$\sqrt{5}$ | D. | $\sqrt{(-2)^{2}}$=-2 |
14. 某几何体的三种视图如图所示,则此几何体是( )
某几何体的三种视图如图所示,则此几何体是( )
 某几何体的三种视图如图所示,则此几何体是( )
某几何体的三种视图如图所示,则此几何体是( )| A. | 圆台 | B. | 圆锥 | C. | 圆柱 | D. | 棱柱 |
15.下列等式从左到右的变形是因式分解的是( )
| A. | 6a2b=2a•3ab | B. | (a+3b)(a-3b)=a2-9 | ||
| C. | 4x2+8x-1=4x(x+2)-1 | D. | ax-ay=a(x-y) |
 如图,OC平分∠AOB,若∠AOC=27°30′,则∠AOB=55度.
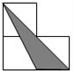
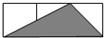
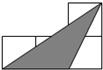
如图,OC平分∠AOB,若∠AOC=27°30′,则∠AOB=55度.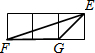 如图,小正方形的边长均为1,则下面4个阴影部分三角形中,能与△EFG相似的是( )
如图,小正方形的边长均为1,则下面4个阴影部分三角形中,能与△EFG相似的是( )