题目内容
17.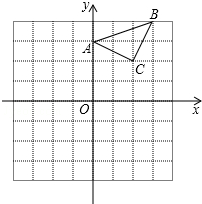 已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).(1)画出△ABC向下平移4个单位长度,再向左平移1个单位长度,得到的△A1B1C1,点C1的坐标是(1,-2);
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是(1,0);
(3)△A2B2C2的面积是10平方单位.
分析 (1)直接利用平移的性质得出各对应点位置进而得出答案;
(2)利用位似图形的性质得出对应点位置进而得出答案;
(3)直接利用△A2B2C2所在矩形面积减去周围三角形面积进而得出答案.
解答  解:(1)如图所示:△A1B1C1,即为所求,
解:(1)如图所示:△A1B1C1,即为所求,
C1(1,-2);
故答案为:(1,-2);
(2)如图所示:△A2B2C2,即为所求,
C2(1,0);
故答案为:(1,0);
(3)△A2B2C2的面积是:4×6-$\frac{1}{2}$×2×6-$\frac{1}{2}$×2×4-$\frac{1}{2}$×2×4=10.
故答案为:10.
点评 此题主要考查了位似变换以及平移变换和三角形面积求法等知识,根据题意得出对应点位置是解题关键.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
17.在平面直角坐标系中,将点A(-2,3)向右平移3个单位长度后得到的对应点A′的坐标是( )
| A. | (1,3) | B. | (-2,-3) | C. | (-2,6) | D. | (-2,1) |
9.一个口袋中有红球、白球共20只,这些球除颜色外都相同,将口袋中的球搅拌均匀,从中随机摸出一只球,记下它的颜色后再放回,不断重复这一过程,共摸了50次,发现有30次摸到红球,则估计这个口块中有红球大约多少只?( )
| A. | 8只 | B. | 12只 | C. | 18只 | D. | 30只 |
6.某种病毒的直径约为0.0000000028米,该直径用科学记数法表示为( )
| A. | 0.28×10-8米 | B. | 2.8×10-10米 | C. | 2.8×10-9米 | D. | 2.8×10-8米 |
 如图,ABCD为正方形,E是BC边上一点,将正方形折叠,使A点与E点重合,折痕为MN.如果tan∠AEN=$\frac{1}{3}$,DC+CE=10,那么△ANE的面积为$\frac{10}{3}$.
如图,ABCD为正方形,E是BC边上一点,将正方形折叠,使A点与E点重合,折痕为MN.如果tan∠AEN=$\frac{1}{3}$,DC+CE=10,那么△ANE的面积为$\frac{10}{3}$.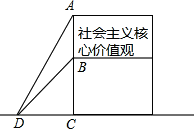 为了弘扬“社会主义核心价值观”,乐至县政府在广场树立公益广告牌,如图所示,为固定广告牌,在两侧加固钢缆,已知钢缆底端D距广告牌立柱距离CD为3米,从D点测得广告牌顶端A点和底端B点的距离分别是5米和$3\sqrt{2}$米.
为了弘扬“社会主义核心价值观”,乐至县政府在广场树立公益广告牌,如图所示,为固定广告牌,在两侧加固钢缆,已知钢缆底端D距广告牌立柱距离CD为3米,从D点测得广告牌顶端A点和底端B点的距离分别是5米和$3\sqrt{2}$米. 如图,若△ADE∽△ACB,AB=4,BC=3,AE=2,则DE=$\frac{3}{2}$.
如图,若△ADE∽△ACB,AB=4,BC=3,AE=2,则DE=$\frac{3}{2}$.