题目内容
12．
如图，若△ADE∽△ACB，AB=4，BC=3，AE=2，则DE=$\frac{3}{2}$．
分析 根据相似三角形的对应边的比相等列出比例式，计算即可．
解答 解：∵△ADE∽△ACB，
∴$\frac{AE}{AB}$=$\frac{DE}{BC}$，即$\frac{2}{4}$=$\frac{DE}{3}$，
解得，DE=$\frac{3}{2}$，
故答案为：$\frac{3}{2}$．
点评 本题考查的是相似三角形的性质，掌握相似三角形的对应边的比相等是解题的关键．
练习册系列答案
相关题目
如图，一木杆在离地某处断裂，木杆顶部落在离木杆底部12米处，已知木杆原长18米，求木杆断裂处离地面多少米？
如图所示，四边形ABCD为矩形（对边相等，四个角是直角），过点D作对角线BD的垂线，交BC的延长线于点E，在BE上取一点F，使DF=EF=4．设AB=x，AD=y，求代数式$\sqrt{{x^2}+{y^2}-8y+16}$的值．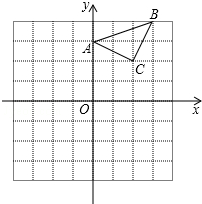
已知：△ABC在直角坐标平面内，三个顶点的坐标分别为A（0，3）、B（3，4）、C（2，2）（正方形网格中每个小正方形的边长是一个单位长度）．
如图是某公司经理和甲、乙工程队长针对一项工程的谈话．问题如下：