题目内容
12.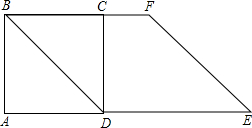 如图,正方形ABCD的边长为4cm,分别在AD、BC的延长线上,四边形BDEF为菱形,则菱形BDEF的面积为16$\sqrt{2}$cm2.
如图,正方形ABCD的边长为4cm,分别在AD、BC的延长线上,四边形BDEF为菱形,则菱形BDEF的面积为16$\sqrt{2}$cm2.
分析 利用勾股定理求出BD,根据菱形的面积公式=DE•CD计算即可.
解答 解:∵四边形ABCD是正方形,
∴AB=AD=DC=4,∠A=90°,
∴BD=$\sqrt{2}$AD=4$\sqrt{2}$,
∵四边形BDEF是菱形,
∴DE=BD=4$\sqrt{2}$,
∴菱形BDEF的面积=DE•CD=16$\sqrt{2}$,
故答案为16$\sqrt{2}$
点评 本题考查菱形的性质、正方形的性质、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.若二元一次方程组$\left\{\begin{array}{l}{2x+5y=a+2}\\{2x+3y=a}\end{array}\right.$的解x,y的和为0,则a的值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | -1 |
17.?ABCD中,如果∠B=60°,则∠D的度数是( )
| A. | 20° | B. | 30° | C. | 60° | D. | 120° |
1.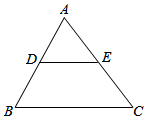 如图,三角形ABC中,D是AB上一点,E是AC上一点,∠ADE=70°,∠B=70°,∠AED=30°,则∠C的度数是( )
如图,三角形ABC中,D是AB上一点,E是AC上一点,∠ADE=70°,∠B=70°,∠AED=30°,则∠C的度数是( )
 如图,三角形ABC中,D是AB上一点,E是AC上一点,∠ADE=70°,∠B=70°,∠AED=30°,则∠C的度数是( )
如图,三角形ABC中,D是AB上一点,E是AC上一点,∠ADE=70°,∠B=70°,∠AED=30°,则∠C的度数是( )| A. | 20° | B. | 30° | C. | 40° | D. | 50° |
 如图,已知△ABC的面积为S,现将△ABC沿CA方向平移CA长度得到△AEF,则四边形CEFB的面积为3S.
如图,已知△ABC的面积为S,现将△ABC沿CA方向平移CA长度得到△AEF,则四边形CEFB的面积为3S.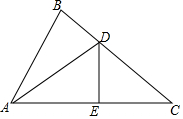 如图,已知∠BAC=60°,∠B=80°,DE垂直平分AC交BC于点D,交AC于E.
如图,已知∠BAC=60°,∠B=80°,DE垂直平分AC交BC于点D,交AC于E.