题目内容
20. 如图,在△ABC中,AB、AC的垂直平分线l1、l2相交于点O,若∠BAC等于82°,则∠OBC=8°.
如图,在△ABC中,AB、AC的垂直平分线l1、l2相交于点O,若∠BAC等于82°,则∠OBC=8°.
分析 连接OA,根据三角形内角和定理求出∠ABC+∠ACB,根据线段垂直平分线的性质、等腰三角形的性质得到∠OAB=∠OBA,∠OAC=∠OCA,根据三角形内角和定理计算即可.
解答 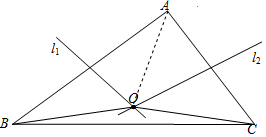 解:连接OA,
解:连接OA,
∵∠BAC=82°,
∴∠ABC+∠ACB=180°-82°=98°,
∵AB、AC的垂直平分线交于点O,
∴OB=OA,OC=OA,
∴∠OAB=∠OBA,∠OAC=∠OCA,
∴∠OBC+∠OCB=98°-(∠OBA+∠OCA)=16°,
∴∠OBC=8°,
故答案为:8.
点评 本题考查的是线段垂直平分线的性质、三角形内角和定理,掌握垂直平分线上任意一点,到线段两端点的距离相等是解题的关键.

练习册系列答案
相关题目
11.如图是某几何体从不同角度看到的图形,这个几何体是( )


| A. | 圆锥 | B. | 圆柱 | C. | 正三棱柱 | D. | 三棱锥 |
8.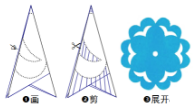 剪纸是中国古老的汉族传统民间艺术之一.下面是制作剪纸的简单流程,展开后的剪纸图案从对称性来判断( )
剪纸是中国古老的汉族传统民间艺术之一.下面是制作剪纸的简单流程,展开后的剪纸图案从对称性来判断( )
 剪纸是中国古老的汉族传统民间艺术之一.下面是制作剪纸的简单流程,展开后的剪纸图案从对称性来判断( )
剪纸是中国古老的汉族传统民间艺术之一.下面是制作剪纸的简单流程,展开后的剪纸图案从对称性来判断( )| A. | 是轴对称图形但不是中心对称图形 | |
| B. | 是中心对称图形但不是轴对称图形 | |
| C. | 既是轴对称图形也是中心对称图形 | |
| D. | 既不是轴对称图形也不是中心对称图形 |
15.与$\sqrt{17}$最接近的整数为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
18.下列四边形中不一定为菱形的是( )
| A. | 对角线相等的平行四边形 | |
| B. | 每条对角线平分一组对角的四边形 | |
| C. | 对角线互相垂直的平行四边形 | |
| D. | 用两个全等的等边三角形拼成的四边形 |
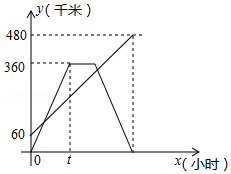 甲、乙两车分别从相距480km的A、B两地相向而行,乙车比甲车先出发1小时,并以各自的速度匀速行驶,途径C地,甲车到达C地停留1小时,因有事按原路原速返回A地.乙车从B地直达A地,两车同时到达A地.甲、乙两车距各自出发地的路程y(千米)与甲车出发所用的时间x(小时)的关系如图,结合图象信息解答下列问题:
甲、乙两车分别从相距480km的A、B两地相向而行,乙车比甲车先出发1小时,并以各自的速度匀速行驶,途径C地,甲车到达C地停留1小时,因有事按原路原速返回A地.乙车从B地直达A地,两车同时到达A地.甲、乙两车距各自出发地的路程y(千米)与甲车出发所用的时间x(小时)的关系如图,结合图象信息解答下列问题: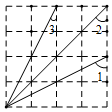 在如图所示的4×4正方形网格中,∠1+∠2+∠3=135°.
在如图所示的4×4正方形网格中,∠1+∠2+∠3=135°.