题目内容
1.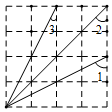 在如图所示的4×4正方形网格中,∠1+∠2+∠3=135°.
在如图所示的4×4正方形网格中,∠1+∠2+∠3=135°.
分析 标注字母,根据图形判断出∠1、∠3是全等直角三角形的两个互余的锐角,∠2为等腰直角三角形的锐角,然后求解即可.
解答 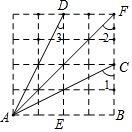 解:如图,在△ABC和△DEA中,$\left\{\begin{array}{l}{AB=DE}\\{∠B=∠AED=90°}\\{BC=AE}\end{array}\right.$,
解:如图,在△ABC和△DEA中,$\left\{\begin{array}{l}{AB=DE}\\{∠B=∠AED=90°}\\{BC=AE}\end{array}\right.$,
∴△ABC≌△DEA(SAS),
∴∠3=∠BAC,
在Rt△ABC中,∠BAC+∠1=90°,
∴∠1+∠3=90°,
由图可知,△ABF是等腰直角三角形,
∴∠2=45°,
∴∠1+∠2+∠3=90°+45°=135°.
故答案为:135.
点评 本题考查了全等图形,等腰直角三角形的性质,准确识图判断出全等三角形是解题的关键.

练习册系列答案
相关题目
7.今年2月份,某市经济开发区完成出口316000000美元,将这个数据316000000用科学记数法表示应为( )
| A. | 316×106 | B. | 31.6×107 | C. | 3.16×108 | D. | 0.316×109 |
6.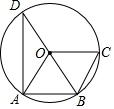 如图,A、B、C、D是⊙O上的四点,BD为⊙O的直径,若四边形ABCO是平行四边形,则∠ADB的大小为( )
如图,A、B、C、D是⊙O上的四点,BD为⊙O的直径,若四边形ABCO是平行四边形,则∠ADB的大小为( )
 如图,A、B、C、D是⊙O上的四点,BD为⊙O的直径,若四边形ABCO是平行四边形,则∠ADB的大小为( )
如图,A、B、C、D是⊙O上的四点,BD为⊙O的直径,若四边形ABCO是平行四边形,则∠ADB的大小为( )| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
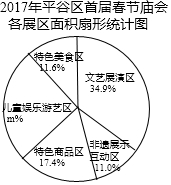 阅读以下材料:
阅读以下材料: 如图,在△ABC中,AB、AC的垂直平分线l1、l2相交于点O,若∠BAC等于82°,则∠OBC=8°.
如图,在△ABC中,AB、AC的垂直平分线l1、l2相交于点O,若∠BAC等于82°,则∠OBC=8°.