题目内容
14.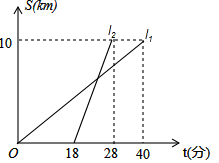 甲、乙两人以相同路线前往距离单位10km的培训中心参加学习,图l1,l2分别表示甲、乙两人前往目的地所走的路程S(千米)随时间t(分)变化的函数图象,以下说法①甲比乙提前12分钟到达;②甲的平均速度为15千米/小时;③甲乙相遇时,乙走了6千米;④乙出发6分钟后追上甲,其中正确的有( )
甲、乙两人以相同路线前往距离单位10km的培训中心参加学习,图l1,l2分别表示甲、乙两人前往目的地所走的路程S(千米)随时间t(分)变化的函数图象,以下说法①甲比乙提前12分钟到达;②甲的平均速度为15千米/小时;③甲乙相遇时,乙走了6千米;④乙出发6分钟后追上甲,其中正确的有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 观察函数图象可知,函数的横坐标表示时间,纵坐标表示路程,然后根据图象上特殊点的意义进行解答.
解答 解:①乙在28分时到达,甲在40分时到达,所以乙比甲提前了12分钟到达;故①错误;
②根据甲到达目的地时的路程和时间知:甲的平均速度=10÷$\frac{40}{60}$=15(千米/时);故②正确;
④设乙出发x分钟后追上甲,则有:$\frac{10}{28-18}$×x=$\frac{10}{40}$×(18+x),解得x=6,故④正确;
③由④知:乙第一次遇到甲时,所走的距离为:6×$\frac{10}{28-18}$=6(km),故③正确;
所以正确的结论有3个,
故选:B.
点评 此题主要考查了一次函数的应用,读函数的图象时首先要理解横纵坐标表示的含义结合图象上点的坐标得出是解题关键.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
2.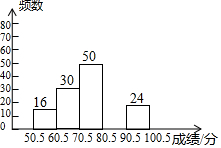 某校组织1000名学生参加“青少年普法知识大赛”,为了了解学生的参赛成绩,从中抽取部分学生的参赛成绩(成绩均为整数)进行统计,并绘制成如下的不完全统计图表.
某校组织1000名学生参加“青少年普法知识大赛”,为了了解学生的参赛成绩,从中抽取部分学生的参赛成绩(成绩均为整数)进行统计,并绘制成如下的不完全统计图表.
请根据所给信息,解答下列问题:
(1)表中m=80,n=0.12;
(2)补全频数分布直方图;
(3)若成绩超过80分为优秀,分别求出被抽取的学生中优秀的学生频数和频率.
 某校组织1000名学生参加“青少年普法知识大赛”,为了了解学生的参赛成绩,从中抽取部分学生的参赛成绩(成绩均为整数)进行统计,并绘制成如下的不完全统计图表.
某校组织1000名学生参加“青少年普法知识大赛”,为了了解学生的参赛成绩,从中抽取部分学生的参赛成绩(成绩均为整数)进行统计,并绘制成如下的不完全统计图表.| 组别 | 分数段 | 频数 | 频率 |
| 一 | 50.5-60.5 | 16 | 0.08 |
| 二 | 60.5-70.5 | 30 | 0.15 |
| 三 | 70.5-80.5 | 50 | 0.25 |
| 四 | 80.5-90.5 | m | 0.40 |
| 五 | 90.5-100.5 | 24 | n |
(1)表中m=80,n=0.12;
(2)补全频数分布直方图;
(3)若成绩超过80分为优秀,分别求出被抽取的学生中优秀的学生频数和频率.
3.已知正比例函数y=(k-2)x的图象经过第一、三象限,则k的值可能是( )
| A. | -2 | B. | 2 | C. | 3 | D. | 0 |

 如图,A、B分别是x轴上位于原点左右两侧的两点,点P(a,4)在第一象限内,一过原点的直线y=2x与直线BD、直线AC同时过点P,直线BD交y轴于点D,且线段AO=2.
如图,A、B分别是x轴上位于原点左右两侧的两点,点P(a,4)在第一象限内,一过原点的直线y=2x与直线BD、直线AC同时过点P,直线BD交y轴于点D,且线段AO=2.
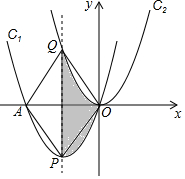 如图,在平面直角坐标系xOy中,抛物线C1的顶点为P(-3,-$\frac{9}{2}$),且过点O(0,0).
如图,在平面直角坐标系xOy中,抛物线C1的顶点为P(-3,-$\frac{9}{2}$),且过点O(0,0).