��Ŀ����
7����ͼ1��������ABCD�У���E��AB����һ���㣨��E���B���غϣ�����E�����Aʱ�˶�ֹͣ����F������BC��һ�㣮�ҡ�EFB=30�㣬��BE=x����BEF��������ABCD�ص����ֵ����ΪS��S����x�ĺ���ͼ����ͼ2��ʾ������0��x��m��m��x��3ʱ�������Ľ���ʽ��ͬ������1����գ�������ABCD�ı߳�Ϊ3��ͼ2��b��ֵΪ$\frac{3}{2}\sqrt{3}$��
��2����S����x�ĺ�����ϵʽ����д��x��ȡֵ��Χ��

���� ��1����ͼ2��֪����x=BE=3ʱ��S�����ֵ����ʱ����E���A�غϣ��ݴ˿ɵ�������ABCD�ı߳�����ͼ2��֪����x=mʱ����F���C�غϣ���ʱ��BF=BC=3��BE=tan30���3=$\sqrt{3}$���ݴ˿ɵ�b��ֵ��
��2���������������0��x��$\sqrt{3}$ʱ����F���߶�BC�ϣ���ʱ����BEF��������ABCD�ص����ּ�Ϊ��BEF����$\sqrt{3}$��x��3ʱ����F��BC���ӳ����ϣ���ʱ����BEF��������ABCD�ص�����Ϊ����BCGE�����ݡ�BEF��������ABCD�ص����ֵ�����ı�ʾ�������ɵ�S����x�ĺ�����ϵʽ��
���  �⣺��1����ͼ2��֪����x=BE=3ʱ��S�����ֵ��
�⣺��1����ͼ2��֪����x=BE=3ʱ��S�����ֵ��
��ʱ����E���A�غϣ���BE=BA=3��
��������ABCD�ı߳�Ϊ3��
��ͼ2��֪����x=mʱ����F���C�غϣ�
��ʱ��BF=BC=3��BE=tan30���3=$\sqrt{3}$��
��S��BEF=$\frac{1}{2}$��$\sqrt{3}$��3=$\frac{3}{2}\sqrt{3}$��
����m=$\sqrt{3}$ʱ��b=$\frac{3}{2}\sqrt{3}$��
�ʴ�Ϊ��3��$\frac{3}{2}\sqrt{3}$��
��2����ͼ1����0��x��$\sqrt{3}$ʱ����F���߶�BC�ϣ�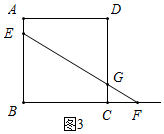
��ʱ����BEF��������ABCD�ص����ּ�Ϊ��BEF��
��BE=x����EFB=30�㣬
��BF=$\sqrt{3}$x��
��S=$\frac{1}{2}$BE��BF=$\frac{1}{2}$��x��$\sqrt{3}$x=$\frac{\sqrt{3}}{2}{x}^{2}$��0��x��$\sqrt{3}$����
��ͼ3����$\sqrt{3}$��x��3ʱ����F��BC���ӳ����ϣ�
��ʱ����BEF��������ABCD�ص�����Ϊ����BCGE��
��BE=x����EFB=30�㣬BC=3��
��BF=$\sqrt{3}$x��CF=$\sqrt{3}$x-3��
��Rt��CFG��CG=x-$\sqrt{3}$��
��S=$\frac{��CG+BE��BC}{2}$=$\frac{1}{2}$��x-$\sqrt{3}$+x����3=3x-$\frac{3}{2}\sqrt{3}$��$\sqrt{3}$��x��3����
����������S����x�ĺ�����ϵʽΪS=$\left\{\begin{array}{l}{\frac{\sqrt{3}}{2}{x}^{2}��0��x��\sqrt{3}��}\\{3x-\frac{3}{2}\sqrt{3}��\sqrt{3}��x��3��}\end{array}\right.$��
���� ������Ҫ�����˶�������ĺ���ͼ��ͨ����ͼ��ȡ��Ϣ���������Խ�������е�ʵ�����⣬��������߷������⡢����������������ͼ��������ʱ���ؼ���Ҫ����ͼ��ĺ��弴��ʶͼ��

| x | m | 0 | 2 |
| y1 | 4 | 3 | t |
| y2 | 6 | n | -1 |
| A�� | -$\frac{1}{3}$ | B�� | -3 | C�� | $\frac{1}{2}$ | D�� | 5 |
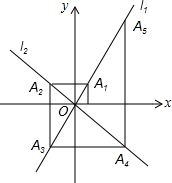 ��ͼ����ƽ��ֱ������ϵ�У�����y=2x��y=-x��ͼ��ֱ�Ϊֱ��l1��l2�����㣨1��0����x��Ĵ��߽�l1�ڵ�A1������A1��y��Ĵ��߽�l2�ڵ�A2������A2��x��Ĵ��߽�l2�ڵ�A3������A3��y��Ĵ��߽�l2�ڵ�A4�������ν�����ȥ�����A2007������Ϊ��21008��21009����
��ͼ����ƽ��ֱ������ϵ�У�����y=2x��y=-x��ͼ��ֱ�Ϊֱ��l1��l2�����㣨1��0����x��Ĵ��߽�l1�ڵ�A1������A1��y��Ĵ��߽�l2�ڵ�A2������A2��x��Ĵ��߽�l2�ڵ�A3������A3��y��Ĵ��߽�l2�ڵ�A4�������ν�����ȥ�����A2007������Ϊ��21008��21009���� ����ABCD�ı�ABΪ5���Խ���ACΪ8��������ABCD�����Ϊ24��
����ABCD�ı�ABΪ5���Խ���ACΪ8��������ABCD�����Ϊ24��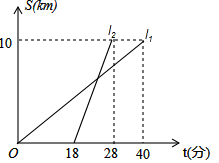 �ס�����������ͬ·��ǰ�����뵥λ10km����ѵ���IJμ�ѧϰ��ͼl1��l2�ֱ��ʾ�ס�������ǰ��Ŀ�ĵ����ߵ�·��S��ǧ�ף���ʱ��t���֣��仯�ĺ���ͼ������˵���ټױ�����ǰ12���ӵ���ڼ�ƽ���ٶ�Ϊ15ǧ��/Сʱ���ۼ�������ʱ��������6ǧ�ף����ҳ���6���Ӻ��ϼף�������ȷ���У�������
�ס�����������ͬ·��ǰ�����뵥λ10km����ѵ���IJμ�ѧϰ��ͼl1��l2�ֱ��ʾ�ס�������ǰ��Ŀ�ĵ����ߵ�·��S��ǧ�ף���ʱ��t���֣��仯�ĺ���ͼ������˵���ټױ�����ǰ12���ӵ���ڼ�ƽ���ٶ�Ϊ15ǧ��/Сʱ���ۼ�������ʱ��������6ǧ�ף����ҳ���6���Ӻ��ϼף�������ȷ���У�������