题目内容
关于x的二次函数y=ax2+bx+c的图象的顶点为P,图象与x轴交于(-1,0)、B(3,0)且△PAB为直角三角形,求二次函数解析式.
考点:待定系数法求二次函数解析式
专题:
分析:根据已知条件得出顶点坐标,然后设出顶点式,将点(1,0)代入从而求得a的值,即得这个二次函数的解析式.
解答:解:∵二次函数y=ax2+bx+c的图象图象与x轴交于(-1,0)、B(3,0),
∴对称轴为:x=1,
∵△PAB为直角三角形,
∴顶点坐标为:(1,2)或(1,-2),
设此二次函数解析式为:y=a(x-1)2+2,或y=a(x-1)2-2,
∴0=a(-1-1)2+2,
解得:a=-
或a=
∴这个二次函数的解析式为y=-
x2+x+
或y=
x2-x-
.
∴对称轴为:x=1,
∵△PAB为直角三角形,
∴顶点坐标为:(1,2)或(1,-2),
设此二次函数解析式为:y=a(x-1)2+2,或y=a(x-1)2-2,
∴0=a(-1-1)2+2,
解得:a=-
| 1 |
| 2 |
| 1 |
| 2 |
∴这个二次函数的解析式为y=-
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
点评:本题考查了用待定系数法求函数解析式的方法,同时还考查了方程组的解法等知识,难度不大.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
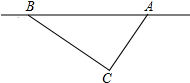 2011年第一季度,我国南方多省市遭遇特大干旱,为了抗旱保收,某市准备开采地下水,经探测2012-01-03 18:36C处地下有水,为此C处需要爆破,已知C处与公路上的停靠站A的距离是300m,与公路上另一停靠站B的距离为400m,且CA垂直CB,为了安全,爆破点C周围250m的范围内禁止进入.问:在进行爆破时,公路AB段是否有危险,是否需要暂时封锁?
2011年第一季度,我国南方多省市遭遇特大干旱,为了抗旱保收,某市准备开采地下水,经探测2012-01-03 18:36C处地下有水,为此C处需要爆破,已知C处与公路上的停靠站A的距离是300m,与公路上另一停靠站B的距离为400m,且CA垂直CB,为了安全,爆破点C周围250m的范围内禁止进入.问:在进行爆破时,公路AB段是否有危险,是否需要暂时封锁?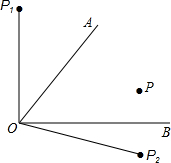 如图,点P是∠AOB内部的一定点.
如图,点P是∠AOB内部的一定点. 如图,已知等边△ABC边长是6,BD=CE=2,BE与AD交于F,求AF的长.
如图,已知等边△ABC边长是6,BD=CE=2,BE与AD交于F,求AF的长.