题目内容
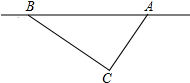 2011年第一季度,我国南方多省市遭遇特大干旱,为了抗旱保收,某市准备开采地下水,经探测2012-01-03 18:36C处地下有水,为此C处需要爆破,已知C处与公路上的停靠站A的距离是300m,与公路上另一停靠站B的距离为400m,且CA垂直CB,为了安全,爆破点C周围250m的范围内禁止进入.问:在进行爆破时,公路AB段是否有危险,是否需要暂时封锁?
2011年第一季度,我国南方多省市遭遇特大干旱,为了抗旱保收,某市准备开采地下水,经探测2012-01-03 18:36C处地下有水,为此C处需要爆破,已知C处与公路上的停靠站A的距离是300m,与公路上另一停靠站B的距离为400m,且CA垂直CB,为了安全,爆破点C周围250m的范围内禁止进入.问:在进行爆破时,公路AB段是否有危险,是否需要暂时封锁?考点:勾股定理的应用
专题:
分析:如图,本题需要判断点C到AB的距离是否小于250米,如果小于等于则有危险,大于则没有危险.因此过C作CD⊥AB于D,然后根据勾股定理在直角三角形ABC中即可求出AB的长度,然后利用三角形的面积公式即可求出CD,然后和250米比较大小即可判断需要暂时封锁.
解答: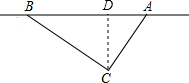 解:如图,过C作CD⊥AB于D,
解:如图,过C作CD⊥AB于D,
∵AC=300米,BC=400米,∠ACB=90°,
∴根据勾股定理得AB=500米,
∵
AB•CD=
BC•AC,
∴CD=240米.
∵240米<250米,故有危险,
因此AB段公路需要暂时封锁.
 解:如图,过C作CD⊥AB于D,
解:如图,过C作CD⊥AB于D,∵AC=300米,BC=400米,∠ACB=90°,
∴根据勾股定理得AB=500米,
∵
| 1 |
| 2 |
| 1 |
| 2 |
∴CD=240米.
∵240米<250米,故有危险,
因此AB段公路需要暂时封锁.
点评:本题考查正确运用勾股定理,善于观察题目的信息是解题以及学好数学的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,△ABD≌△CDB,若AB∥CD,则AB的对应边是( )
如图,△ABD≌△CDB,若AB∥CD,则AB的对应边是( )| A、DB | B、BC | C、CD | D、AD |
下列各式中正确的是( )
A、
| ||
B、
| ||
C、±
| ||
D、
|
 如图,已知∠B=∠C=∠BAD,∠ADC=∠DAC,AE⊥BC,求∠DAE的度数.
如图,已知∠B=∠C=∠BAD,∠ADC=∠DAC,AE⊥BC,求∠DAE的度数.