题目内容
 已知反比例函数y=
已知反比例函数y=| k |
| x |
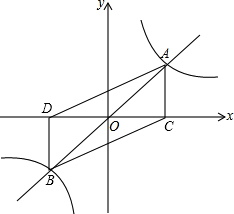
(1)分别过A,B两点向x轴作垂线,垂足分别为C,D,求证:四边形ACBD是平行四边形;
(2)若m=1,k=2,求出线段AB的长;
(3)若m,k分别满足 ①、②两式:
m2-5m+1=0…①;
关于x的方程
| 5 |
| x-2 |
| k |
| x2-4 |
| 2 |
| x+2 |
试求:(i)m+
| 1 |
| m |
(ii) 以AB为等腰直角三角形的斜边的面积.
考点:反比例函数综合题
专题:
分析:(1)利用关于原点对称点的性质得出BD
AC进而得出答案;
(2)将m=1,k=2代入得出,进而得出A,B点坐标,进而利用勾股定理求出即可;
(3)利用增根的定义以及等腰直角三角形的性质得出等腰直角三角形的斜边的面积即可.
| ∥ |
. |
(2)将m=1,k=2代入得出,进而得出A,B点坐标,进而利用勾股定理求出即可;
(3)利用增根的定义以及等腰直角三角形的性质得出等腰直角三角形的斜边的面积即可.
解答:解:(1)∵反比例函数y=
(k>0)与正比例函数y=mx(m>0)相交于A、B 两点,
分别过A,B两点向x轴作垂线,垂足分别为C,D,
∴点A,B关于O点对称,
∴BD=AC,
又∵BD∥AC,
∴BD
AC,
∴四边形ACBD是平行四边形;
(2)∵
,
解得:
或
,
∴AB=2
=2
=4;
(3)(i)∵m2-5m+1=0,
∴m-5+
=0,
∴m+
=5,
(ii)∵关于x的方程
-
=
有增根,
∴5(x+2)-k=2(x-2),
整理得出:x=
,
∴
=2或-2,
∴k=8或20,
∵以AB为等腰直角三角形的斜边的面积,
∴s=
AB2=
×4k(m+
)=40或100.
| k |
| x |
分别过A,B两点向x轴作垂线,垂足分别为C,D,
∴点A,B关于O点对称,
∴BD=AC,
又∵BD∥AC,
∴BD
| ∥ |
. |
∴四边形ACBD是平行四边形;
(2)∵
|
解得:
|
|
∴AB=2
| AC2+OC2 |
| 2+2 |
(3)(i)∵m2-5m+1=0,
∴m-5+
| 1 |
| m |
∴m+
| 1 |
| m |
(ii)∵关于x的方程
| 5 |
| x-2 |
| k |
| x2-4 |
| 2 |
| x+2 |
∴5(x+2)-k=2(x-2),
整理得出:x=
| k-14 |
| 3 |
∴
| k-14 |
| 3 |
∴k=8或20,
∵以AB为等腰直角三角形的斜边的面积,
∴s=
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| m |
点评:此题主要考查了反比例函数的综合应用以及勾股定理以及分式方程的增根和平行四边形的判定等知识,得出k的值是解题关键.

练习册系列答案
相关题目
 某校准备将两幢教学楼间一块长30m、宽20m的长方形空地,建成一个矩形花园.为方便同学们行走和观赏,准备在花园中修两条纵向平行和一条横向弯折的小道,剩余的地方种植花草.如图,要使种植花草的面积为532m2,那么小道的宽度应为多少米?(注:阴影部分表示道路,所有小道的宽度相等,且每段小道均为平行四边形)
某校准备将两幢教学楼间一块长30m、宽20m的长方形空地,建成一个矩形花园.为方便同学们行走和观赏,准备在花园中修两条纵向平行和一条横向弯折的小道,剩余的地方种植花草.如图,要使种植花草的面积为532m2,那么小道的宽度应为多少米?(注:阴影部分表示道路,所有小道的宽度相等,且每段小道均为平行四边形)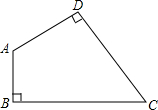 如图,四边形ABCD中,∠A=135°,∠B=∠D=90°,BC=2
如图,四边形ABCD中,∠A=135°,∠B=∠D=90°,BC=2