题目内容
16.下列说法中,正确的是( )| A. | sin60°+cos30°=1 | |
| B. | 若α为锐角,则$\sqrt{(sinα-1)^{2}}$﹦1-sinα | |
| C. | 对于锐角β,必有sinβ<cosβ | |
| D. | 在Rt△ABC中,∠C=90°,则有tanAcosB=1 |
分析 根据各个选项中的说法可以判断它们是否正确,从而可以解答本题.
解答 解:sin60°+cos30°=$\frac{\sqrt{3}}{2}+\frac{\sqrt{3}}{2}=\sqrt{3}$,故选项A错误;
若α为锐角,则$\sqrt{(sinα-1)^{2}}$﹦|sinα-1|=1-sinα,故选项B正确;
若β=60°,则sin60°>cos60°,故选项C错误;
在Rt△ABC中,∠C=90°,则有tanAcosB=$\frac{a}{b}•\frac{a}{c}=\frac{{a}^{2}}{bc}$,故选项D错误;
故选B.
点评 本题考查特殊角的三角函数值、锐角三角函数,解题的关键是明确题意,可以判断题目中的语句是否正确.

练习册系列答案
相关题目
4.小红上学要经过三个十字路口,每个路口遇到红、绿灯的机会都相等,小红希望上学时经过每个路口都是绿灯,但实际这样的概率是( )
| A. | 0.125 | B. | 0.5 | C. | 0.375 | D. | 1.5 |
11. 如图,已知在?ABCD中,AE⊥BC于点E,以点B为中心,取旋转角等于∠ABC,把△BAE顺时针旋转,得到△BA′E′,连接DA′.若∠ADC=60°,AD=5,DC=4 则DA′的大小为( )
如图,已知在?ABCD中,AE⊥BC于点E,以点B为中心,取旋转角等于∠ABC,把△BAE顺时针旋转,得到△BA′E′,连接DA′.若∠ADC=60°,AD=5,DC=4 则DA′的大小为( )
 如图,已知在?ABCD中,AE⊥BC于点E,以点B为中心,取旋转角等于∠ABC,把△BAE顺时针旋转,得到△BA′E′,连接DA′.若∠ADC=60°,AD=5,DC=4 则DA′的大小为( )
如图,已知在?ABCD中,AE⊥BC于点E,以点B为中心,取旋转角等于∠ABC,把△BAE顺时针旋转,得到△BA′E′,连接DA′.若∠ADC=60°,AD=5,DC=4 则DA′的大小为( )| A. | 1 | B. | $\sqrt{6}$ | C. | $\sqrt{21}$ | D. | 2$\sqrt{3}$ |
1.圆锥的底面半径是2cm,母线长为6cm,则这个圆锥的侧面展开后得到的扇形圆心角的度数为( )
| A. | 60° | B. | 120° | C. | 45° | D. | 135° |
5.下列计算正确的是( )
| A. | x6÷x2=x3 | B. | x3•x2=x6 | C. | (x3)2=x6 | D. | a2+a3=a5 |
6.两圆的半径分别为3和5,它们的圆心之间的距离为6,则这两个圆的位置关系是 ( )
| A. | 外离 | B. | 外切 | C. | 相交 | D. | 内切 |
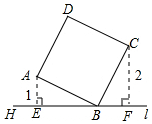 如图,直线l过正方形ABCD的顶点B,点A、C到直线l的距离AE、CF分别是1cm、2cm,则线段EF的长为3cm.
如图,直线l过正方形ABCD的顶点B,点A、C到直线l的距离AE、CF分别是1cm、2cm,则线段EF的长为3cm. 如图,△ABC中,AB=5,AC=4,BD平分∠ABC,CD平分∠ACB,过点D作BC的平行线,交AB于点M,将AC于点N,则△AMN的周长为9.
如图,△ABC中,AB=5,AC=4,BD平分∠ABC,CD平分∠ACB,过点D作BC的平行线,交AB于点M,将AC于点N,则△AMN的周长为9.