题目内容
11. 如图,已知在?ABCD中,AE⊥BC于点E,以点B为中心,取旋转角等于∠ABC,把△BAE顺时针旋转,得到△BA′E′,连接DA′.若∠ADC=60°,AD=5,DC=4 则DA′的大小为( )
如图,已知在?ABCD中,AE⊥BC于点E,以点B为中心,取旋转角等于∠ABC,把△BAE顺时针旋转,得到△BA′E′,连接DA′.若∠ADC=60°,AD=5,DC=4 则DA′的大小为( )| A. | 1 | B. | $\sqrt{6}$ | C. | $\sqrt{21}$ | D. | 2$\sqrt{3}$ |
分析 过A′作A′F⊥DA于点F,由旋转的性质可得求得A′B,在Rt△ABE中可求得BE,则可求得A′E,则可求得DF和A′F,在Rt△A′FD中由勾股定理可求得A′D.
解答 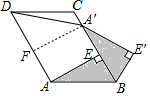 解:
解:
∵四边形ABCD为平行四边形,
∴AB=CD=4,∠ABC=∠ADC=60°,
∴BE=$\frac{1}{2}$AB=2,AE=A′F=$\frac{\sqrt{3}}{2}$AB=2$\sqrt{3}$,
∵取旋转角等于∠ABC,把△BAE顺时针旋转,得到△BA′E′,
∴A′B在线段BC上,且A′B=AB=4,
∴A′E=A′B-BE=4-2=2,
∴AF=A′E=2,
∴DF=DA-AF=5-2=3,
在Rt△A′FD中,由勾股定理可得A′D=$\sqrt{A′{F}^{2}+D{F}^{2}}$=$\sqrt{(2\sqrt{3})^{2}+{3}^{2}}$=$\sqrt{21}$,
点评 本题主要考查旋转的性质及勾股定理的应用,构造直角三角形是解题的关键.

练习册系列答案
相关题目
16.下列说法中,正确的是( )
| A. | sin60°+cos30°=1 | |
| B. | 若α为锐角,则$\sqrt{(sinα-1)^{2}}$﹦1-sinα | |
| C. | 对于锐角β,必有sinβ<cosβ | |
| D. | 在Rt△ABC中,∠C=90°,则有tanAcosB=1 |
3. 小聪用直尺和圆规作角平分线,方法如下:①利用三角板上的刻度,在OA和OB上分别截取OM、ON,使OM=ON;②分别过M、N作OM、ON的垂线,交于点P;③作射线OP,则OP为∠AOB的平分线,小聪用尺规作角平分线时,用到的三角形全等的判定方法是( )
小聪用直尺和圆规作角平分线,方法如下:①利用三角板上的刻度,在OA和OB上分别截取OM、ON,使OM=ON;②分别过M、N作OM、ON的垂线,交于点P;③作射线OP,则OP为∠AOB的平分线,小聪用尺规作角平分线时,用到的三角形全等的判定方法是( )
 小聪用直尺和圆规作角平分线,方法如下:①利用三角板上的刻度,在OA和OB上分别截取OM、ON,使OM=ON;②分别过M、N作OM、ON的垂线,交于点P;③作射线OP,则OP为∠AOB的平分线,小聪用尺规作角平分线时,用到的三角形全等的判定方法是( )
小聪用直尺和圆规作角平分线,方法如下:①利用三角板上的刻度,在OA和OB上分别截取OM、ON,使OM=ON;②分别过M、N作OM、ON的垂线,交于点P;③作射线OP,则OP为∠AOB的平分线,小聪用尺规作角平分线时,用到的三角形全等的判定方法是( )| A. | SSS | B. | SAS | C. | ASA | D. | HL |
20.中国药学家屠呦呦发明的青蒿素为保护人类健康做出了重大贡献,荣获2015年诺贝尔生理学或医学奖,奖金约为3 020 000元人民币.将3 020 000用科学记数法表示为( )
| A. | 3.02×104 | B. | 302×104 | C. | 3.02×106 | D. | 302×106 |
1.已知∠A=60°,则∠A的补角是( )
| A. | 30° | B. | 60° | C. | 120° | D. | 180° |
 如图,点C.F,A,D在同一条直线上,CF=AD,AB∥DE,AB=DE.
如图,点C.F,A,D在同一条直线上,CF=AD,AB∥DE,AB=DE. 如图,一副三角板(直角顶点重合)摆放在桌面上,若∠AOD=140°,则∠AOC=55°;∠BOC=35°.
如图,一副三角板(直角顶点重合)摆放在桌面上,若∠AOD=140°,则∠AOC=55°;∠BOC=35°. 如图,一位同学做了一个斜面装置进行科学实验,△ABC是该装置左视图,∠ACB=90°,∠B=15°,为了加固斜面,在斜面AB的中点D处连结一条支撑杆CD,量得CD=6.
如图,一位同学做了一个斜面装置进行科学实验,△ABC是该装置左视图,∠ACB=90°,∠B=15°,为了加固斜面,在斜面AB的中点D处连结一条支撑杆CD,量得CD=6. 如图,在△ABC中,BA=BC,∠ABC=90°,AD∥BC,点E在边AC上,且∠DEB=90°,DH⊥AC于H.
如图,在△ABC中,BA=BC,∠ABC=90°,AD∥BC,点E在边AC上,且∠DEB=90°,DH⊥AC于H.