题目内容
15.在Rt△ABC中,∠C=90°,已知c=10,则a2+b2+c2=200.分析 先根据勾股定理求出a2+b2的值,进而可得出结论.
解答 解:∵在Rt△ABC中,∠C=90°,c=10,
∴a2+b2=102=100,
∴a2+b2+c2=100+100=200.
故答案为:200.
点评 本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
10.已知直角三角形两边的长为6和8,则此三角形的周长为( )
| A. | 24 | B. | 14+2$\sqrt{7}$ | C. | 24或14+2$\sqrt{7}$ | D. | 以上都不对 |
7.四边形ABCD中,对角线AC与BD交于点O,下列条件不能判定这个四边形是平行四边形的是( )
| A. | AD=BC,AB=DC | B. | OA=OC,OB=OD | C. | AB∥DC,AD=BC | D. | ∠A=∠C,∠B=∠D |
5.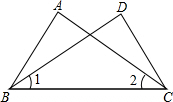 如图,已知∠1=∠2,则下列条件中,不能使△ABC≌△DBC成立的是( )
如图,已知∠1=∠2,则下列条件中,不能使△ABC≌△DBC成立的是( )
 如图,已知∠1=∠2,则下列条件中,不能使△ABC≌△DBC成立的是( )
如图,已知∠1=∠2,则下列条件中,不能使△ABC≌△DBC成立的是( )| A. | AB=CD | B. | AC=BD | C. | ∠A=∠D | D. | ∠ABC=∠DBC |
 如图是由五个边长为1的正方形组成的图象,如果把它们剪拼成一个正方形,那么所拼成的正方形边长的平方是多少?边长是有理数吗?请画出示意图.
如图是由五个边长为1的正方形组成的图象,如果把它们剪拼成一个正方形,那么所拼成的正方形边长的平方是多少?边长是有理数吗?请画出示意图.