题目内容
20.计算:(1)$\frac{\sqrt{18}+\sqrt{2}}{\sqrt{2}}$-3
(2)2$\sqrt{3}$+$\sqrt{27}$-$\sqrt{\frac{1}{3}}$
(3)(7+4$\sqrt{3}$)(2-$\sqrt{3}$)2
(4)($\sqrt{3}$-$\sqrt{2}$)($\sqrt{3}$+$\sqrt{2}$)-1.
分析 (1)先把$\sqrt{8}$化简,然后合并后进行二次根式的除法运算;
(2)先把各二次根式化为最简二次根式,然后合并即可;
(3)先利用完全平方公式计算,然后利用平方差公式计算;
(4)利用平方差公式计算.
解答 解:(1)原式=$\frac{3\sqrt{2}+\sqrt{2}}{\sqrt{2}}$-3
=4-3
=1;
(2)原式=2$\sqrt{3}$+3$\sqrt{3}$-$\frac{\sqrt{3}}{3}$
=$\frac{14\sqrt{3}}{3}$;
(3)原式=(7+4$\sqrt{3}$)(7-4$\sqrt{3}$)
=49-48
=1;
(4)原式=3-2-1
=0.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
相关题目
11.用两张大小及形状均相同的直角三角形纸片拼图,可拼成( )种不同的图形.
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
8.某摩托车厂本周内计划每日生产300辆摩托车,由于工人实行轮休,每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表(增加的车辆数为正数,减少的车辆数为负数)
(1)本周三生产了多少辆摩托车?
(2)本周总生产量与计划生产量相比,是增加还是减少?
(3)星期几产量最多,星期几产量最少?相差多少辆?
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | -5 | +7 | -3 | +4 | +10 | -9 | -25 |
(2)本周总生产量与计划生产量相比,是增加还是减少?
(3)星期几产量最多,星期几产量最少?相差多少辆?
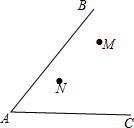 如图,南开中学高二年级的学生分别在五云山寨M,N两处参加社会时间活动.先要在道路AB,AC形成的锐角∠BAC内设一个休息区P,使P到两条道路的距离相等,并且使得PM=PN,请用直尺和圆规作出P点的位置(不写作法,值保留作图痕迹).
如图,南开中学高二年级的学生分别在五云山寨M,N两处参加社会时间活动.先要在道路AB,AC形成的锐角∠BAC内设一个休息区P,使P到两条道路的距离相等,并且使得PM=PN,请用直尺和圆规作出P点的位置(不写作法,值保留作图痕迹).