题目内容
5.a,b为有理数,且满足等式a+b$\sqrt{3}$=$\sqrt{6}$•$\sqrt{1+\sqrt{4+2\sqrt{3}}}$,则a+b的值为( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
分析 利用完全平方公式将$\sqrt{1+\sqrt{4+2\sqrt{3}}}$逐步化简为$\frac{\sqrt{2}}{2}$($\sqrt{3}$+1),代入等式得出a+b$\sqrt{3}$=3+$\sqrt{3}$,从而得出答案.
解答 解:∵$\sqrt{4+2\sqrt{3}}$=$\sqrt{(\sqrt{3})^{2}+2\sqrt{3}+1}$=$\sqrt{(\sqrt{3}+1)^{2}}$=$\sqrt{3}$+1,
∴$\sqrt{1+\sqrt{4+2\sqrt{3}}}$=$\sqrt{1+\sqrt{3}+1}$=$\sqrt{2+\sqrt{3}}$=$\sqrt{\frac{1}{2}(4+2\sqrt{3})}$=$\sqrt{\frac{1}{2}(\sqrt{3}+1)^{2}}$=$\frac{\sqrt{2}}{2}$($\sqrt{3}$+1),
则$\sqrt{6}$•$\sqrt{1+\sqrt{4+2\sqrt{3}}}$=$\sqrt{6}$×$\frac{\sqrt{2}}{2}$($\sqrt{3}$+1)=$\sqrt{3}$($\sqrt{3}$+1)=3+$\sqrt{3}$,
∴a+b$\sqrt{3}$=3+$\sqrt{3}$,
则a=3,b=1,
∴a+b=4,
故选:B.
点评 本题主要考查实数的混合运算,熟练掌握完全平方公式是解题的关键.

练习册系列答案
相关题目
15. 如图,直线y=x+1与y轴交于点A1,依次作正方形A1B1C1O、正方形A2B2C2C1、…、正方形AnBnCnCn-1,使得点A1、A2、…,An在直线x+1上,点C1、C2、…,Cn在x轴上,则点Bn的坐标是( )
如图,直线y=x+1与y轴交于点A1,依次作正方形A1B1C1O、正方形A2B2C2C1、…、正方形AnBnCnCn-1,使得点A1、A2、…,An在直线x+1上,点C1、C2、…,Cn在x轴上,则点Bn的坐标是( )
 如图,直线y=x+1与y轴交于点A1,依次作正方形A1B1C1O、正方形A2B2C2C1、…、正方形AnBnCnCn-1,使得点A1、A2、…,An在直线x+1上,点C1、C2、…,Cn在x轴上,则点Bn的坐标是( )
如图,直线y=x+1与y轴交于点A1,依次作正方形A1B1C1O、正方形A2B2C2C1、…、正方形AnBnCnCn-1,使得点A1、A2、…,An在直线x+1上,点C1、C2、…,Cn在x轴上,则点Bn的坐标是( )| A. | (2n-1,2n-1) | B. | (2n-1+1,2n-1) | C. | (2n-1,2n-1) | D. | (2n-1,n) |
20.如果a与8互为相反数,那么a是( )
| A. | $\frac{1}{8}$ | B. | -$\frac{1}{8}$ | C. | 8 | D. | -8 |
10.已知圆锥的侧面积为15π,底面半径为3,则圆锥的高为( )
| A. | 3 | B. | 4 | C. | 5 | D. | 7 |
17.下列是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
15.已知函数y=ax2-2ax-1(a是常数,a≠0),下列结论正确的是( )
| A. | 当a=1时,函数图象经过点(-1,1) | |
| B. | 当a=-2时,函数图象与x轴没有交点 | |
| C. | 若a<0,函数图象的顶点始终在x轴的下方 | |
| D. | 若a>0,则当x≥1时,y随x的增大而增大 |
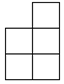
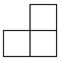
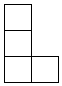
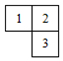 由6个大小相同的小正方体组合成一个几何体,其俯视图如图所示,其中正方形中的数字表示该位置放置的小正方体的个数,则该几何体的主视图为( )
由6个大小相同的小正方体组合成一个几何体,其俯视图如图所示,其中正方形中的数字表示该位置放置的小正方体的个数,则该几何体的主视图为( )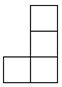
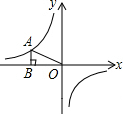 如图,一支反比例函数y=$\frac{k}{x}$的图象经过点A,作AB⊥x轴于点B,连接OA,若S△AOB=3,则k的值为( )
如图,一支反比例函数y=$\frac{k}{x}$的图象经过点A,作AB⊥x轴于点B,连接OA,若S△AOB=3,则k的值为( )