题目内容
10.已知圆锥的侧面积为15π,底面半径为3,则圆锥的高为( )| A. | 3 | B. | 4 | C. | 5 | D. | 7 |
分析 设圆锥的母线长为l,根据圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和扇形面积公式得到$\frac{1}{2}$•2π•3•l=15π,然后求出l后利用勾股定理计算圆锥的高.
解答 解:设圆锥的母线长为l,
根据题意得$\frac{1}{2}$•2π•3•l=15π,解得l=5,
所以圆锥的高=$\sqrt{{5}^{2}-{3}^{2}}$=4.
故选B.
点评 本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.

练习册系列答案
相关题目
1.若从多边形的一个顶点可以引出七条对角线,则这个多边形是( )
| A. | 七边形 | B. | 八边形 | C. | 九边形 | D. | 十边形 |
18. 如图,在边长为2的菱形ABCD中,∠A=60°,DE⊥AB,DF⊥BC,则△DEF的周长为( )
如图,在边长为2的菱形ABCD中,∠A=60°,DE⊥AB,DF⊥BC,则△DEF的周长为( )
 如图,在边长为2的菱形ABCD中,∠A=60°,DE⊥AB,DF⊥BC,则△DEF的周长为( )
如图,在边长为2的菱形ABCD中,∠A=60°,DE⊥AB,DF⊥BC,则△DEF的周长为( )| A. | 3 | B. | $\sqrt{3}$ | C. | 6 | D. | $3\sqrt{3}$ |
15.若分式$\frac{2ab}{a+b}$中的a、b的值同时扩大到原来的3倍,则分式的值( )
| A. | 不变 | B. | 是原来的3倍 | C. | 是原来的6倍 | D. | 是原来的9倍 |
2.化简$\frac{{a}^{2}b}{b-a}$+$\frac{a{b}^{2}}{a-b}$结果正确的是( )
| A. | a-b | B. | b-a | C. | ab | D. | -ab |
19.一组数据:6,4,a,3,2,它的平均数是4,则它的中位数与方差分别是( )
| A. | 4和2 | B. | 4.5和$\sqrt{2}$ | C. | 4和$\sqrt{2}$ | D. | 4.5和2 |
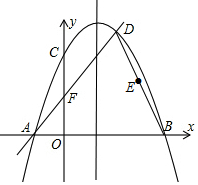 已知,如图二次函数y=ax2+bx+c(a≠0)的图象与y轴交于点C(0,4)与x轴交于点A、B,点B(4,0),抛物线的对称轴为x=1.直线AD交抛物线于点D(2,m).
已知,如图二次函数y=ax2+bx+c(a≠0)的图象与y轴交于点C(0,4)与x轴交于点A、B,点B(4,0),抛物线的对称轴为x=1.直线AD交抛物线于点D(2,m).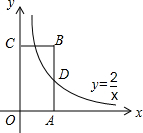 如图,反比例函数y=$\frac{2}{x}$的图象经过矩形OABC的边AB的中点D,则矩形OABC的面积为4.
如图,反比例函数y=$\frac{2}{x}$的图象经过矩形OABC的边AB的中点D,则矩形OABC的面积为4.