题目内容
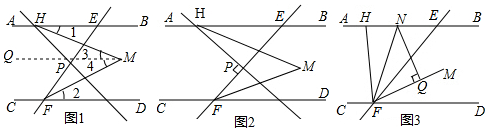
2.如图,已知直线AB∥CD,直线EF分别与AB、CD相交于点E、F,FM平分∠EFD,点H是射线EA上一动点(不与点E重合),过点H的直线交EF于点P,HM平分∠BHP交FM于点M.(1)如图1,试说明:∠HMF=$\frac{1}{2}$(∠BHP+∠DFP);
请在下列解答中,填写相应的理由:
解:过点M作MQ∥AB(过直线外一点有且只有一条直线与这条直线平行).
∵AB∥CD(已知),
∴MQ∥CD(如果两条直线都和第三条直线平行,那么这两条直线也互相平行)
∴∠1=∠3,∠2=∠4(两直线平行,内错角相等)
∴∠1+∠2=∠3+∠4(等式的性质)
即∠HMF=∠1+∠2.
∵FM平分∠EFD,HM平分∠BHP(已知)
∵∠1=$\frac{1}{2}$∠BHP,∠2=$\frac{1}{2}$∠DFP(角平分线定义)
∴∠HMF=$\frac{1}{2}$∠BHP+$\frac{1}{2}$∠DFP=$\frac{1}{2}$(∠BHP+∠DFP)(等量代换).
(2)如图2,若HP⊥EF,求∠HMF的度数;
(3)如图3,当点P与点F重合时,FN平分∠HFE交AB于点N,过点N作NQ⊥FM于点Q,试说明无论点H在何处都有∠EHF=2∠FNQ.
分析 (1)根据两直线平行,内错角相等,以及角平分线定义进行判断即可;
(2)先根据HP⊥EF,AB∥CD,得到∠EHP+∠DFP=90°,再根据(1)中结论即可得到∠HMF的度数;
(3)先根据题意得到∠NFQ=90°-∠FNQ,再根据FN平分∠HFE,FM平分∠EFD,即可得出∠HFD=2∠NFQ,最后根据∠EHF+∠HFD=180°,即可得出∠EHF=2∠FNQ.
解答 解:(1)由MQ∥CD,得到∠1=∠3,∠2=∠4,其依据为:两直线平行,内错角相等;
由FM平分∠EFD,HM平分∠BHP,得到∠1=$\frac{1}{2}$∠BHP,∠2=$\frac{1}{2}$∠DFP,其依据为:角平分线定义.
故答案为:两直线平行,内错角相等;角平分线定义.
(2)如图2,∵HP⊥EF,
∴∠HPE=90°,
∴∠EHP+∠HEP=180°-90°=90°(三角形的内角和等于180°)
又∵AB∥CD,
∴∠HEP=∠DFP.
∴∠EHP+∠DFP=90°.
由(1)得:∠HMF=$\frac{1}{2}$(∠EHP+∠DFP)=$\frac{1}{2}$×90°=45°.
(3)如图3,∵NQ⊥FM,
∴∠NFQ+∠FNQ=180°-90°=90°(三角形的内角和等于180°).
∴∠NFQ=90°-∠FNQ.
∵FN平分∠HFE,FM平分∠EFD,
又∵∠NFQ=∠NFE+∠QFE=$\frac{1}{2}$(∠HFE+∠EFD)=$\frac{1}{2}$∠HFD,
∴∠HFD=2∠NFQ.
又∵AB∥CD,
∴∠EHF+∠HFD=180°,
∴∠EHF=180°-∠HFD=180°-2∠NFQ=180°-2(90°-∠FNQ)=2∠FNQ,
即无论点H在何处都有∠EHF=2∠FNQ.
点评 本题主要考查了平行线的性质与判定,角平分线的定义以及平行公理的运用,解决问题的关键是掌握:两直线平行,内错角相等;两直线平行,同旁内角互补.

| A. | 2a% | B. | 1+2a% | C. | (2+a%)a% | D. | (1+a%)2 |