题目内容
16.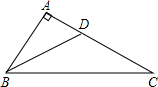 在△ABC中,∠A=90°,BD是△ABC的角平分线,AB=8cm,BD=10cm,则点D到BC的距离为6cm.
在△ABC中,∠A=90°,BD是△ABC的角平分线,AB=8cm,BD=10cm,则点D到BC的距离为6cm.
分析 根据题意作辅助线,然后根据角平分线的性质得出DE=AD,根据已知可得AD=2,所以DE=2,即D点到BC的距离是2.
解答  解:过点D作DE⊥BC于点E,
解:过点D作DE⊥BC于点E,
∵已知∠A=90°,BD是∠ABC的平分线,DE⊥BC,
∴∠A=∠DEB=90°,
根据角平分线的性质可得:DE=AD.
∵AB=8cm,BD=10cm,
∴DA=6cm.
∴DE=6cm,即D点到BC的距离是6cm,
故答案为6.
点评 本题主要考查角平分线的性质,作出辅助线是解决本题的关键,难度适中.

练习册系列答案
相关题目
4.一个人从A地出发向北偏东80°方向到达B地,再从B地向北偏西25°方向到达C地,如果∠ACB=55°,则∠CAB的度数是( )
| A. | 25° | B. | 50° | C. | 70° | D. | 75° |
1.如(2x+m)与(4x+3)的乘积中不含x的一次项,则m的值为( )
| A. | -$\frac{3}{2}$ | B. | $\frac{3}{2}$ | C. | -$\frac{2}{3}$ | D. | $\frac{2}{3}$ |
5.已知一个等腰三角形一边长为4cm,另一边长为6cm,那么这个等腰三角形的周长为( )
| A. | 14cm | B. | 16cm | C. | 14cm或16cm | D. | 以上都不对 |
6.计算$\frac{1}{3}$a2•(-6ab)的结果正确的是( )
| A. | -2a2b | B. | 2a2b | C. | -2a3b | D. | 2a3b |

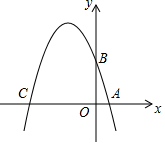 如图,在平面直角坐标系xOy中,A、B、C三点分别为坐标轴上的三个点,且OA=1,OB=3,OC=4.
如图,在平面直角坐标系xOy中,A、B、C三点分别为坐标轴上的三个点,且OA=1,OB=3,OC=4.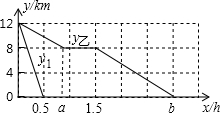 某景区内从甲地到乙地的路程是12km,小华步行从甲地到乙地游玩,速度为5km/h,走了4km后,中途休息了一段时间,然后继续按原速前往乙地,景区从甲地开往乙地的电瓶车每隔半小时发一趟车,速度是24km/h,若小华与第1趟电瓶车同时出发,设小华距乙地的路程为y乙(km),第n趟电瓶车距乙地的路程为yn(km),n为正整数,行进时间为x(h).如图画出了y乙,y1与x的函数图象.
某景区内从甲地到乙地的路程是12km,小华步行从甲地到乙地游玩,速度为5km/h,走了4km后,中途休息了一段时间,然后继续按原速前往乙地,景区从甲地开往乙地的电瓶车每隔半小时发一趟车,速度是24km/h,若小华与第1趟电瓶车同时出发,设小华距乙地的路程为y乙(km),第n趟电瓶车距乙地的路程为yn(km),n为正整数,行进时间为x(h).如图画出了y乙,y1与x的函数图象.