题目内容
12.△ABC中,∠ACB=90°,AC=8.(1)如图1,若AC=BC,∠MCN=45°,交BA及延长线分别于N、M,若AM=2$\sqrt{2}$,求MN的值;
(2)如图2,将△ABC绕C点旋转一个角度到△DEC,直线AD、EB交于P点,Q是BC中点,连PQ,在旋转过程中,当BC=6时,求:①∠BPA的度数;②PQ的最大值.

分析 (1)作AF⊥AB,使AF=BE,连接DF,根据SAS证得△CAF≌△CBE和△CDF≌△CDE,再由勾股定理和等量代换即可解答.
(2)①设∠BCE=∠ACD=α,可得∠CBE=∠CEB=∠CAD=∠CDA=90°-$\frac{1}{2}$α,根据四边形内角和可得∠BPA=90°;
②取AB的中点K,连接PK、QK,则KQ=$\frac{1}{2}$AC=4,PK=AB=5,继而可得PQ≤KP+KQ=9.
解答 解:(1)如图,
证明:过点A作AF⊥AB,使AF=BN,连接MF,
∵在△ABC中,AC=BC,∠ACB=90°,
∴∠CAB=∠B=45°,
∴∠FAC=45°,
∴△CAF≌△CBN(SAS),
∴CF=CN,
∠ACF=∠BCN,
∵∠BCN+∠ACN=90°,
∴∠ACF+∠ACN=90°,即∠FCN=90°,
∵∠MCN=45°,
∴∠MCF=45°,
∴∠MCF=∠MCN,
又∵CM=CM,
∴△CMF≌△CMN(SAS),
∴MF=MN,
∵AM2+AF2=MF2,
∴AM2+BN2=MN2.
在Rt△ABC中,AC=BC=8,∴AB=8$\sqrt{2}$,
∴BN=AB-AN=AB-(MN-AM)=8$\sqrt{2}$-MN+2$\sqrt{2}$=10$\sqrt{2}$-MN,∴(2$\sqrt{2}$)2+(10$\sqrt{2}$-MN)2=MN2,
∴MN=5.7$\sqrt{2}$.
(2)解:①∵△DEC是由△ABC绕C点旋转得到,
∴CE=CB,CD=CA,∠BCE=∠ACD,
设∠BCE=∠ACD=α∴∠CBE=∠CEB=∠CAD=∠CDA=90°-$\frac{1}{2}$α,
∴在四边形BCDP中,∠BPA=360°-90°-α-2(90°-$\frac{1}{2}$α)=90°;
②∵在Rt△ABC中,∠ACB=90°,BC=6,AC=8,
∴AB=10,
如图1, 取AB的中点K,连接PK、QK,
取AB的中点K,连接PK、QK,
则KQ=$\frac{1}{2}$AC=4,PK=AB=5,
∴PQ≤KP+KQ=9,
∴PQ的最大值是9.
点评 此题是几何变换综合题,主要考查了旋转的性质,勾股定理及三角形全等的判定与性质,直角三角形的性质及中位线定理,解(1)的关键是构造全等三角形△CAF≌△CBN,构建以PQ为边的三角形,根据三角形三边关系得出PQ的长度范围是解(2)的关键.

| A. | 小于零 | B. | 等于零 | C. | 大于零 | D. | 不能确定 |
| A. | 36.1 | B. | 11.4 | C. | 361 | D. | 114 |
| A. | 25° | B. | 50° | C. | 70° | D. | 75° |
| A. | -$\frac{3}{2}$ | B. | $\frac{3}{2}$ | C. | -$\frac{2}{3}$ | D. | $\frac{2}{3}$ |
 为了支援地震灾区同学,某校开展捐书活动,九(1)班同学积极参与,现将捐书数量绘制成频数分布直方图(如图所示),如果捐书数量在3.5-4.5组别的频率是0.3,那么捐书数量在4.5-5.5组别的人数是16.
为了支援地震灾区同学,某校开展捐书活动,九(1)班同学积极参与,现将捐书数量绘制成频数分布直方图(如图所示),如果捐书数量在3.5-4.5组别的频率是0.3,那么捐书数量在4.5-5.5组别的人数是16.
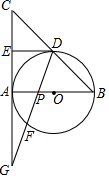 如图,△ABC中,AB=AC,点D为BC边的中点,且DE⊥AC于点E,以AB为直径作⊙O,F是⊙O上一点,DF交AB于点P,DF的延长线交射线CA于点G.
如图,△ABC中,AB=AC,点D为BC边的中点,且DE⊥AC于点E,以AB为直径作⊙O,F是⊙O上一点,DF交AB于点P,DF的延长线交射线CA于点G.