题目内容
已知:如图,在平行四边形ABCD中,AE是BC边上的高,将△ABE沿BC方向平移,使点E与点C重合,得△GFC.
(1)求证:BE=DG;
若∠B=60°,当AB与BC满足什么数量关系时,四边形ABFG是菱形?证明你的结论.
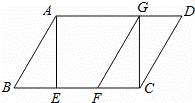
(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD.
∵AE是BC边上的高,且CG是由AE沿BC方向平移而成.
∴CG⊥AD.
∴∠AEB=∠CGD=90°.
∵AE=CG,
∴Rt△ABE≌Rt△CDG(HL).
∴BE=DG;
解:当BC= AB时,四边形ABFG是菱形.
AB时,四边形ABFG是菱形.
证明:∵AB∥GF,AG∥BF,
∴四边形ABFG是平行四边形.
∵Rt△ABE中,∠B=60°,
∴∠BAE=30°,
∵四边形ABFG是菱形,
∴AB=BF,
∴EF= AB,
AB,
∵BE=CF,
∴BC= AB.
AB.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
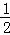 x+b与反比例函数y=
x+b与反比例函数y=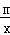 在第二象限的图象交于A(n,
在第二象限的图象交于A(n,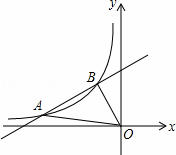
 沿弦AC翻折交AB于点D,连接CD.如果∠BAC=20°,则∠BDC=( )
沿弦AC翻折交AB于点D,连接CD.如果∠BAC=20°,则∠BDC=( )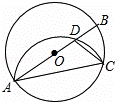
 ﹣1)0+(﹣1)2015﹣2sin30°.
﹣1)0+(﹣1)2015﹣2sin30°. B.
B.  C.
C.  D.
D. 
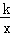 相交于A、B两点,A点的坐标为(1,2),AC⊥x轴于C,连结BC.
相交于A、B两点,A点的坐标为(1,2),AC⊥x轴于C,连结BC.